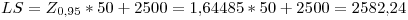Examen Final - 61.09. Probabilidad y Estadística B - 28/02/2008
Cátedra: Única
Fecha: 4º Oportunidad - (2º Cuatrimestre 2007)
Día: 28/02/2008
Tema: 2
Enunciado
Punto 1
En una ruta de 100 km se midieron las fallas en 5 intervalos disjuntos de 1 km obteniéndose los siguientes resultados: 22, 23 , 24, 26, 30. Plantear un modelo para la cantidad de fallas por kilómetro de ruta y dar aproximadamente un intervalo de 0.9 de confianza para la cantidad de fallas en toda la ruta.
Punto 2


Cero para otro x.
Dadas las muestras 3.1 y 2.3, hallar la expresión analítica de la función de verosimilitud y graficarla. Hallar el estimador máximo verosímil del parámetro a.
Punto 3
Se desea verificar si la proporción de piezas defectuosas producidas por una máquina esta dentro de límites aceptables (hasta 2%). Explicar detalladamente como deben hacerse los ensayos.
Punto 4
Sean  y
y 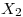 variables aleatorias independientes con funciones de densidad uniformes en el intervalo [a;a+1] y [b;b+1] respectivamente. Hallar la función de densidad de
variables aleatorias independientes con funciones de densidad uniformes en el intervalo [a;a+1] y [b;b+1] respectivamente. Hallar la función de densidad de  .
.
Punto 5
Se quieren colocar 4 ventanas en una casa. La probabilidad de que un vidrio se rompa mientras es transportado es 0.01. La probabilidad de que un vidrio se rompa mientras es colocado es 0.02. Hallar la cantidad mínima de vidrios que deben fabricarse para tener 0.9 de probabilidad de colocar los 4 vidrios en la casa. AYUDA: El número de vidrios necesario es chico.
Resolución
Punto 1
Primero propongo un modelo para “cantidad de fallas en un tramo de 1 km de ruta”. La distribución mas común para este tipo de problemas es una Poisson. Como los tramos son de 1km de longitud, 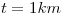 , entonces el modelo es X=“cantidad de fallas en un tramo de 1 km de ruta” ~ Poisson(
, entonces el modelo es X=“cantidad de fallas en un tramo de 1 km de ruta” ~ Poisson( ).
).
Usando un estimador de máxima verosimilitud para un parámetro, se le puede aplicar una función y así obtener el estimador de MV para otro parámetro. Usando  para estimar
para estimar 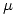 se puede obtener una estimación de
se puede obtener una estimación de  , ya que
, ya que 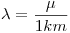
Los valores de la muestra son 22, 23, 24, 26, 30, entonces  ⇒
⇒ 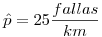
Ahora hay que buscar un intervalo de confianza del 90% de NC.
Si llamamos Y a la cantidad de fallas en toda la ruta, 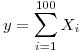 . Por T.C.L.,
. Por T.C.L.,  .
.
 , según la estimación, y como
, según la estimación, y como 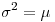 para una Poisson,
para una Poisson, 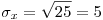 ⇒
⇒ 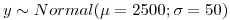
Llamo 
Ahora planteo el intervalo de confianza del 90% para la Z estándar, un intervalo simétrico porque f(z) es simétrica:

Reemplazo Z y despejo:

Entonces:
Punto 2
Primero hay que plantear la función de máxima verosimilitud,  .
.

Desarrollando:
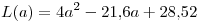
Dado que 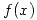 está definida para
está definida para 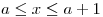 , despejo el intervalo de posibles valores de
, despejo el intervalo de posibles valores de  .
.
- De
 ,
,  tiene que ser menor que todos los
tiene que ser menor que todos los  de la muestra, entonces
de la muestra, entonces  .
. - De
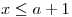 ,
,  tiene que ser mayor que todos los
tiene que ser mayor que todos los  de la muestra, restándoles uno, entonces
de la muestra, restándoles uno, entonces  .
.
La función 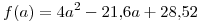 es una parábola, graficándola queda:
es una parábola, graficándola queda:
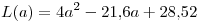 es el mismo gráfico, pero restringiendo para
es el mismo gráfico, pero restringiendo para 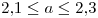 , entonces el gráfico de
, entonces el gráfico de 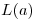 es:
es:
Por último, el estimador de M.V. de  es el
es el  que maximiza
que maximiza 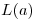 , entonces
, entonces 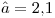
 , que, como se ve en el gráfico, es el
, que, como se ve en el gráfico, es el  que minimiza
que minimiza 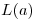 . Además, da un valor para
. Además, da un valor para  que no cae dentro de la región válida de
que no cae dentro de la región válida de 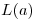 .
.
Punto 3
Punto 4
Como  y
y 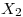 son dos variables uniformes definidas en intervalos de longitud 1, sus funciones de densidad de probabilidad son
son dos variables uniformes definidas en intervalos de longitud 1, sus funciones de densidad de probabilidad son  para ambas, y como son independientes
para ambas, y como son independientes  .
.
Defino:
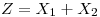 (la variable que pide el enunciado)
(la variable que pide el enunciado)
 (podría ser otra)
(podría ser otra)
Transformo la región de  usando
usando 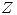 y
y  y tengo este gráfico:
y tengo este gráfico:
Ahora hay que buscar 
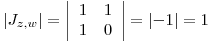 . Entonces
. Entonces 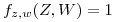 .
.
Ahora calculo 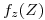 . Viendo el gráfico hay que dividir la función en dos intervalos, porque cambian los límites entre los que se mueve
. Viendo el gráfico hay que dividir la función en dos intervalos, porque cambian los límites entre los que se mueve  :
:
Para 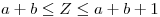

Para 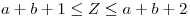

Punto 5
Defino los eventos R='Se rompe un vidrio', T='Se rompe un vidrio al trasladarlo' y C='Se rompe un vidrio al colocarlo'.
Primero calculo 
Ahora llamo  a la cantidad de vidrios rotos de la cantidad total que se fabriquen (
a la cantidad de vidrios rotos de la cantidad total que se fabriquen ( vidrios), entonces
vidrios), entonces  .
.
Tengo que buscar un  tal que
tal que 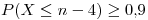 , es decir, la probabilidad de que 4 o mas no se rompan tiene que ser igual (o mayor) a
, es decir, la probabilidad de que 4 o mas no se rompan tiene que ser igual (o mayor) a 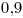 . Como el enunciado dice que la cantidad de vidrios es chica, conviene probar distintos valores de
. Como el enunciado dice que la cantidad de vidrios es chica, conviene probar distintos valores de  , ya que si se quiere calcular, hay que resolver
, ya que si se quiere calcular, hay que resolver 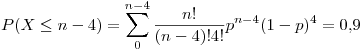 y es muy complicado hallar ese
y es muy complicado hallar ese  .
.
- Para

 , así que
, así que  no sirve.
no sirve.
- Para

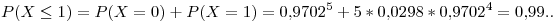 , entonces con 5 vidrios alcanza.
, entonces con 5 vidrios alcanza.