Examen Final - 61.09. Probabilidad y Estadística B

Cátedra: Todas
Fecha: Tercera Oportunidad - Segundo Cuatrimestre 2006
Día: 08/02/2007
Tema: 2

Una empresa pesquera tiene un costo mensual de $100000. Se sabe que la cantidad pescada por dia corresponde a una v.a. exponencial de media 4Ton. El precio del mercado es de 1 $/kg con probabilidad de 0,25; 1,2 $/kg con probabilidad de 0,6; 1,4 $/kg con probabilidad de 0,15. ¿Cuál es la probabilidad de perder dinero?

Una oficina de empleados afirma que los dias posteriores a un partido la cantidad de ausentes se incrementa. Generalmente el ausentismo es de un 4%. La oficina tiene 70 empleados. Elabore un test para probar la afirmación y expliquelo para que el gerente de la empresa lo entienda.

Se sabe que la v.a. X tiene la siguiente distribución:

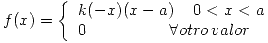
Determine k. Estime en forma Bayesiana el parámetro “a” si se tienen las siguientes muestras: 4; 4,2; 5. Explicar los resultados obtenidos.

Se quiere hacer una fiesta para diez invitados y se desea entregar un regalo a todos aquellos que se queden hasta el final. La probabilidad de que una persona se quede hasta el final es de 0,2. Calcular, sabiendo que vienen los 10 invitados, la mínima cantidad de regalos que se deben comprar para que la probabilidad de que no alcancen sea de 3%. Recalcular ahora si la probabilidad de que falten a la fiesta es de 0,5.

Se sabe que X tiene una cierta distribución f(x). Se tiene una muestra de volumen 5: X(1), X(2), X(3), X(4), X(5). Hallar la distribución de X(3) en función de f(x).