Examen Final - 61.09. Probabilidad y Estadística B

Cátedra: Todas
Fecha: Primer Oportunidad - Primer Cuatrimestre 2006
Día: 05/07/2006
Tema: 1

El contenido de los paquetes de cereal llenados por una determinada máquina tiene una distribución Normal, con desvío estándar de 30grs. Se desea establecer el control períodico del procesos de llenado y se establece en 5% la probabilidad de detener la máquina cuando el peso promedio de los paquetes sea de 360grs. (que es el peso neto indicado en el envase) y en 2% la probabilidad de no detenerla cuando el peso promedio difiere en un 10% del valor indicado en el envase.

1. Indique el criterio de decisión y el tamaño de la muestra adecuada que darúa Ud. a la persona encargada de controlar el proceso.

La longitud (en metros) de ciertas varillas es una variable aleatoria con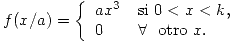

1. Determine K
2. Estime, en forma Bayessiana, y presente un intervalo de confianza para el parámetro “a”, si en una muestra de 4 varillas se obtuvieron las siguientes longitudes en metros: 1, 1, 4, 2.
3. Con esta información calcule la probabilidad de que una varilla mida más de 4 metros.

Dos segmentos de linea AB y CD tienen longitudes de 8 y 6 cm. respectivamente. Dos puntos P y Q se eligen sobre AB y CD respectivamente.

1. Halle la función de probabilidad del área del triángulo de altura AP y base CQ.
2. ¿Cuál es el varlor esperado del área del triángulo de altura AP y base CQ?

Ciertos usuarios de internet reciben mensajes del sevidor A en un 60% de las veces y del servidor B en un 40% de las veces. Los mensajes enviados por A llegan con intervalo de tiempo exponencial, según un proceso Poisson con una tasa de 3 mensajes por día, mientras que los de B tienen una tasa de 4 mensajes por día.

1. En un lapso de un día y medio se reciben 4 mensajes de un mismo servidor. ¿Cuál es la probabilidad de que sean de A?
2. Suponga que ciertos usuarios reciben sólo mensajes de A. Deje indicado el cálculo de la probabilidad de que el sexto mensaje se reciba antes de 2 días.

El peso de cierto producto es una variable aleatoria con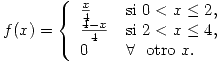

Se venden sólo los productos con peso menor a 2Kg. El precio de venta es de $3 y el costo es de $.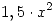

1. ¿Cuál es la función de densidad de probabilidad de la ganancia por cada producto que se vende?
2. Calcule la probabilidad de que al vender 36 productos, la ganacia sea mayor a $20