Examen Final - 61.09. Probabilidad y Estadística B

Cátedra: Todas
Fecha: Segunda Fecha - Segundo Cuatrimestre 2005 - Tema 3
Día: 21/12/2005

Un acopiador de citricos tiene almacenada al principio de la semana un total de X (en toneladas) de naranjas con X variable uniforme [0,4]. El peso total (en toneladas) de lo que vende en una semana es una variable aleatoria uniforme Y. Tenga en cuenta que lo que vende en una semana es menor o igual que lo que hay en el acopiador al comienzo de la semana.

1. Si en una semana vendio 3.5 toneladas ¿Cual es la probabilidad de que al principio de la semana el acopiador haya tenido almacenado más de 3.8 toneladas?
2. Deje indicado en detalle el cálculo de la covarianza de las variables X e Y.

El peso medio de ciertos citricos recogidos de determinada plantacion debe estar comprendido entre 150 y 200 gr. Además, el porcentaje de cítricos podridos no debe superar el 15%. Para controlar que los cítricos cumplen con lo especificado, se toma una muestra de 10 cítricos, obteniendose 2 cítricos podridos y los siguientes pesos en gramos: 185,188,190,195,205,145,150,168,170,180.

1. Establezca los criterios para decidir si los cítricos cumplen la especificación.
2. Indique los riesgos al decidir. Trace dos puntos a elección de la curva característica: uno para el peso y otro para el porcentaje de cítricos podridos.
3. Indique suposiciones que debe realizar, si las hubiere, para resolver el problema.

Un sistema tiene 3 componentes conectados en serie. La duración de cada componente es una variable exponencial negativa de media 0.5 meses si es de calidad A y de media 1 mes si es de calidad B.

1. En el 30% de las veces se arma el sistema con solo componentes calidad A y en el resto de las veces con los de calidad B. ¿Cual es la función de distribución de la duración del sistema?
2. La probabilidad de que un componente sea de A es 0,40 y que un componente sea de calidad B es de 0,6. ¿Cual es la probabilidad de que un sistema con elementos mezclados dure más de 1 mes?

La cantidad de litros de gaseosa que un pico de llenado envía a una lata es una variable aleatoria cuya función de densidad de probabilidad es:

La capacidad de cada lata es de 0,5 litros. Considere que el rebalse se pierde.

1. ¿Cual es la probabilidad de que la cantidad total de litros perdidos al llenar 30 latas supere los 6 litros?

Suponga que el número de defectos en una cinta magnética de grabación de 50 metros es una variable Poisson de media 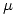desconocida. Se seleccionan 5 cintas al azar y se cuenta el número de defectos en cada una resultando: 0, 2, 3, 1, 1.

1. Estime en forma bayesiana, mediante un intervalo del 90% de confianza, la cantidad media de defectos de la cinta. Suponga a priori que la distribución de la media 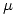es una variable exponencial de media 0,2.