Examen Final - 61.09. Probabilidad y Estadística B

Cátedra: Todas
Fecha: Primera Oportunidad - Primer Cuatrimestre 2004
Día: 07/07/2004

El tiempo neto en pista (sin entrar a boxes), que tarda un corredor de fórmula 1 en realizar una carrera, es una variable aleatoria uniforme U(70,90) minutos. Se detiene una sóla vez en un box tardando un tiempo aleatorio según una distribución uniforme U(60,90) segundos. El tiempo neto en pista y el tiempo en el box son variables independientes. Antes de comenzar la carrera, el corredor da una vuelta previa que le insume 4 minutos.

1. Halle la función de densidad del tiempo total que tarda el corredor en realizar la carrera, incluyendo la vuelta previa.
2. Si durante la carrera se detiene en boxes 4 veces, ¿cuál es la media y el desvío estándar del tiempo total de la carrera, incluyendo la vuelta previa?

El diámetro de ciertos ejes es una variable aleatoria cuya función de densidad es es:

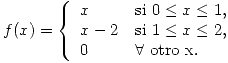
Se venden ejes cuyos diámetros sean superiores a 1cm. El precio de venta (en $) de cada uno de éstos es 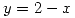, y el costo es de $0,1.

1. ¿Cuál es la función de densidad de probabilidad del precio de venta de cada eje?
2. ¿Cuál es la probabilidad de que al vender 30 ejes la ganancia sea menor que $16?

El 60% de los rollos de tela de un negocio son importados de un cierto país, mientras que el 40% son de industria nacional. Las fallas que se producen en rollos importados de 100 metros de tela, siguen un Proceso Poisson de modo tal que la probabilidad de que tengan alguna es 0,9; mientras que los rollos de industria nacional presentan en promedio 0,03 fallas por metro.

1. Al revisar 10 rollos de 100 metros de un mismo origen, se encontraron 7 con más de una falla. ¿Cuál es la probabilidad de que se hayan revisado rollos importados?
2. Se revisan rollos de 100 metros importados. ¿Cuál es la probabilidad de que el sexto revisado sea el cuarto con más de una falla?

En una empresa de servicios de cable, el porcentaje de abonados incobrables es tradicionalmente del 12%. Para verificar si dicho porcentaje ha aumentado en el último mes, (y en ese caso contratar personal especializado que se ocupe del tema) se decide establecer en 0,05 la probabilidad de contratar el personal si el porcentaje no aumentó, y en 0,10 la probabilidad de dejar las cosas como están, aún cuando en realidad dicho porcentaje haya subido al 16%. Indique el criterio de decisión y el tamaño de la muestra adecuado que daría Ud. para satisfacer las condiciones establecidas.

El peso (en Kg.) de ciertas piezas es una V.A. con 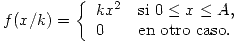, siendo .

1. Determine A
2. Estime en forma Bayessiana, mediante un intervalo de confianza, el parámetro “k”, si en una muestra de cuatro piezas se obtuvieron los siguientes pesos en Kg.: 1, 3, 1, 2.
3. Calcule la probabilidad de que una pieza pese menos de 3Kg.