Examen Final - 61.09. Probabilidad y Estadística B
- Enunciado
  - Punto I
  - Punto II
  - Punto III
  - Punto IV
  - Punto V
- Resolución
  - Punto I
- Discusión

Examen Final - 61.09. Probabilidad y Estadística B

Cátedra: Todas
Fecha: Quinta Oportunidad - Segundo Cuatrimestre 2000
Día: 25/02/2001

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Punto I

Un escrito tiene 200 palabras. La probabilidad de que una palabra esté mal escrita es del 3%.

Calcular la P de que el escrito no tenga errores.
Si la P de encontrar cada error es del 90% y el tiempo para corregir cada error es N(4;1)seg.
1. Calcular la P de que se detecten 5 errores
2. Calcular la P de que el tiempo para corregir los errores detectados sea menor a 30 segundos.
3. Encontrar la P(x) de la cantidad de errores remanentes en el escrito y su media.

Para demostrar que un remedio es efectivo para curar determinada enfermedad en por lo menos el 80% de las personas, debe realizarse también una prueba con placebo (falso remedio inofensivo). El ministerio de salud pública exige que sea demostrada la efectividad con riesgo de error menor a 0,5%. Describa los pasos necesarios para demostrar esta afirmación y explique cuantitativamente los riesgos que se corren. Invente valores y desarrolle un ejemplo.

Punto III

Estime el parámetro b (máximo) de una variable uniforme de variancia 1/12 si se obtuvieron 8; 7,2 y 7,6 como valores muestrales.

Punto IV

El precio p de un producto en el mercado es una v.a. uniforme entre 8 y 12. La demanda depende del precio según la función $<tex>f(d/p) = e^{-(d-p)}</tex>$ para $<tex>d > p</tex>$ . Encontrar f(d) y la P de que la demanda supere 14.

Punto V

Demostrar qué variable es y si $<tex>y = \sqrt{x}</tex>$ siendo x una variable gamma de parámetros $<tex>k = 1/2</tex>$ y $<tex>\lambda = 1/2</tex>$ .

Resolución

Punto I

Sabemos que, para una palabra 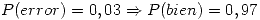$<tex>P(error) = 0,03 \Rightarrow P(bien) = 0,97</tex>$

Nos piden $<tex>P(\mbox{ningun error}) = P((1bien) \cap \cdots \cap (200bien)) = 0,97^{200} \cong 2.26x10^{-3}</tex>$

En el segundo punto nos piden 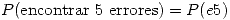$<tex>P(\mbox{encontrar 5 errores}) = P(e5)</tex>$

Sabemos que: 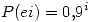$<tex>P(ei) = 0.9^i</tex>$

Pero luego pensamos: para encontrar 5 errores, se deben haber producido, por lo menos 5 errores. La probabilidad de que ocurran i errores es una binomial de parámetro 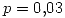$<tex>p = 0.03</tex>$ . Luego $<tex>P(\mbox{haya i errores}) = P(hi) = {200 \choose i}\cdot 0.03^i \cdot 0.97^{200-i}</tex>$

Por lo tanto:

$<tex>P(e5) = P((h5 \cap e5) \cup \cdots \cup (h200 \cap e5)) = 0.9^5 \cdot \sum_{i=5}^{200} {200 \choose i} \cdot 0.03^i \cdot 0.97^{200-i} = 0.9^5 \cdot 200! \cdot \sum_{i=5}^{200} \frac{0.03^i \cdot 0.97^{200-i}}{i! \cdot (200 - i)!}</tex>$

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.