Examen Parcial - 61.08. Àlgebra - Sin datos de fecha ni tema
Enunciado
1) (a) Sea 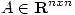 una matriz de rango
una matriz de rango  y
y 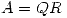 una descomposición QR normalizada de A, i) ¿qué dimensión y qué rango tiene
una descomposición QR normalizada de A, i) ¿qué dimensión y qué rango tiene  ?, ii)deducir que
?, ii)deducir que  y que
y que 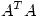 es inversible.
es inversible.
(b) Sabiendo que ![<tex> \left[{\begin{array}{cc}1 & 1 \\-1 & 1 \\1 & 0\end{array}}\right]\left[{\begin{array}{ccc}\sqrt{3} & -\sqrt{3} & 0 \\0 & \sqrt{2} & -2\sqrt{2}\end{array}}\right]</tex> <tex> \left[{\begin{array}{cc}1 & 1 \\-1 & 1 \\1 & 0\end{array}}\right]\left[{\begin{array}{ccc}\sqrt{3} & -\sqrt{3} & 0 \\0 & \sqrt{2} & -2\sqrt{2}\end{array}}\right]</tex>](lib/plugins/latex/images/3c328e740b65bf1adc52d49e137634d31b07e189_0.png) y
y
![<tex>b=[\begin{array}{ccc}\sqrt{3} & -\sqrt{3} & \sqrt{3}\end{array}]^T</tex> <tex>b=[\begin{array}{ccc}\sqrt{3} & -\sqrt{3} & \sqrt{3}\end{array}]^T</tex>](lib/plugins/latex/images/8a6d02f42a60072812f72a02977f678dfbb44c4f_0.png) ,hallar la matriz de proyección a
,hallar la matriz de proyección a 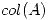 y todos los
y todos los 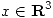 que minimicen
que minimicen 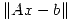 .
.
2) (a) Sea 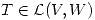 y
y 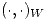 un producto interno en
un producto interno en  . Demostrar que
. Demostrar que 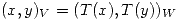 , es un producto interno en
, es un producto interno en  si y sólo si
si y sólo si  es inyectiva.
b) Demostrar que
es inyectiva.
b) Demostrar que 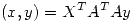 con
con ![<tex>A=\left[{\begin{array}{cc}1 & 1 \\1 & 2 \\0 & 1\end{array}}\right]</tex> <tex>A=\left[{\begin{array}{cc}1 & 1 \\1 & 2 \\0 & 1\end{array}}\right]</tex>](lib/plugins/latex/images/b45157c165587ae0813b05190bf2cc89308fa91d_0.png) es un producto interno en
es un producto interno en 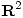 . (Sugerencia: use (a)).
. (Sugerencia: use (a)).
3)Sean  y
y 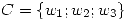 bases de los espacios vectoriales
bases de los espacios vectoriales  y
y  respectivamente.
respectivamente.
(a)Justificar la existencia de una única transformación lineal 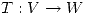 que verifica
que verifica 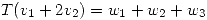 ,
, 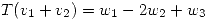 y
y 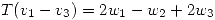 y encontrar bases de
y encontrar bases de  y de
y de  .
.
(b) Encontrar bases  de
de  y
y 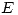 de
de  tales que
tales que ![<tex>[T]_{DE}</tex> <tex>[T]_{DE}</tex>](lib/plugins/latex/images/66841754aeec885ae2c977d5aa0e77ef502264bd_0.png) tenga tantas columnas y filas nulas como sea posible.
tenga tantas columnas y filas nulas como sea posible.
4)Sea 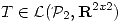 definida por
definida por 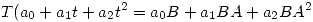 con
con 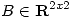 inversible y
inversible y ![<tex>A=\left[{\begin{array}{cc}1 & \alpha \\-\alpha & 1\end{array}}\right]</tex> <tex>A=\left[{\begin{array}{cc}1 & \alpha \\-\alpha & 1\end{array}}\right]</tex>](lib/plugins/latex/images/892fe3440a358e1e313be1d4990cad8164e13687_0.png) .
.
(a) Hallar los valores de  para los cuales
para los cuales 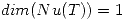
(b) Considerando 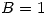 ,
,  y el producto interno en
y el producto interno en 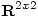 ,
, 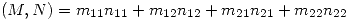 , expresar
, expresar ![<tex>C=\left[{\begin{array}{cc}1 & 2 \\0 & 0\end{array}}\right]</tex> <tex>C=\left[{\begin{array}{cc}1 & 2 \\0 & 0\end{array}}\right]</tex>](lib/plugins/latex/images/5e17aa49a478a0a6a93c017bae294d20b7722eb6_0.png) como
como 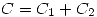 , con
, con 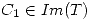 y
y 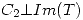
El examen se aprueba resolviendo correctamente cuatro puntos. Justificar todas las respuestas.
