Examen Parcial - 61.08. Álgebra II

Examen Parcial - 61.08. Álgebra II

Cátedra: Todas
Fecha: Primera Oportunidad - Primer Cuatrimestre 2013
Día: 18/05/2013

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Determinar si las siguientes afirmaciones son verdaderas o falsas (con demostración o contraejemplo respectivamente):
1. Si $<tex>A=\{u_1,u_2,...,u_k\}</tex>$ y $<tex>B=\{v_1,v_2,...,v_k\}</tex>$ son dos conjuntos incluidos en un espacio vectorial $<tex>V</tex>$ $<tex>\Rightarrow gen(A \cap B) = gen(A) \cap gen(B)</tex>$ .
2. Sean $<tex>V</tex>$ y $<tex>W</tex>$ $<tex>\mathbf{R}</tex>$ -espacios vectoriales, $<tex>T_1: V \to W</tex>$ y $<tex>T_2:V \to W</tex>$ transformaciones lineales. Si $<tex>Nu (T_1) = Nu(T_2)</tex>$ e $<tex>Im(T_1) = Im(T_2) \Rightarrow T_1 = T_2</tex>$ .
Sea $<tex>T \in \mathcal{L}(P_2, \mathbf{R}^4): [T]_{BC} = \begin{pmatrix}1 & k & 0\\ 0 & 1 & k+2\\ -1 & 0 & -1 \end{pmatrix}</tex>$ con $<tex>C=\left \lbrace\begin{pmatrix}1\\0\\0\end{pmatrix},\begin{pmatrix}-1\\0\\1\end{pmatrix},\begin{pmatrix}0\\1\\1\end{pmatrix}\right \rbrace</tex>$ base de $<tex>\mathbf{R}^4</tex>$ y $<tex>B=\{1,1+t,1+t^2\}</tex>$ base de $<tex>P_2</tex>$ .
1. ¿Es posible hallar $<tex>k \in \mathbf{R}</tex>$ de modo que existan $<tex>p,q \in P_2</tex>$ tales que $<tex>p \neq q</tex>$ y $<tex>T(p) = T(q)= (1\; 0\; -1)^t</tex>$ ?
Sea $<tex>B=\{v_1,v_2\}</tex>$ base de un espacio vectorial real $<tex>V</tex>$ con producto interno $<tex>(\cdot,\cdot)</tex>$ . Sean $<tex>(v_1, 2v_2)=\left \| v_2 \right \|^2 = \left \| v_1 \right \|^2 = 3</tex>$ y $<tex>S=gen \{v_1 -v_2\}</tex>$ .
1. Calcular la distancia de $<tex>w=3v_1 + 3v_2</tex>$ al subespacio $<tex>S</tex>$
2. Calcular la matriz del producto interno en base $<tex>B^\ast=\{v_1+v_2, v_1-v_2\}</tex>$ .
Sean $<tex>A=\begin{pmatrix}1 & 0 & 1 & 0\\ 0 & 0 & 0 & 2\\ 1 & 0 & 1 & 2\end{pmatrix}</tex>$ y $<tex>B \in \mathbf{R}^{4\times 2}</tex>$ una matriz de rango $<tex>1</tex>$ tales que $<tex>Col(B)\subseteq Nul(A)</tex>$ y el vector $<tex>(1\; 0\; 0\; 0)^t</tex>$ pertenece al espacio nulo de $<tex>\mathbf{B}^t</tex>$ .
1. Sabiendo que $<tex>\frac{4}{3} col_1 A + \frac{1}{6} col_4 A = P_{Col(A)} \begin{pmatrix}1 \\0 \\2\end{pmatrix}</tex>$ hallar todos los $<tex>\hat{x} \in \mathbf{R}^4</tex>$ que minimizan $<tex>\left \| A x- \begin{pmatrix}1\\0\\2\end{pmatrix} \right \|, \forall x \in \mathbf{R}^4</tex>$ .
Sea $<tex>V=\{f: \mathbf{R} \to \mathbf{R} / f(x) = a\, g_1(x) + b\, g_2(x),\, a,b \in \mathbf{R}\}</tex>$ , donde $<tex>g_1(x) = e^x</tex>$ y $<tex>g_2(x) = x e^x</tex>$ , con el producto interno $<tex>(f,g)=\int_{-1}^{1} {e^{-2x} f(x) g(x) dx}</tex>$ Sea $<tex> T \in \mathcal(V, \mathbf{R}^{2\times 2})</tex>$ de modo tal que: $<tex>T(g_1 + g_2) = \begin{pmatrix} (g_1, g_2) & 0\\1&3\left\|g_2\right\|^2\end{pmatrix}</tex>$ y $<tex>T(g_1 - g_2) = \begin{pmatrix} 0&(g_1, g_2)\\-\frac{3}{8}\left\|g_1+g_2\right\|^2 & -\frac{1}{2}\left\|g_1\right\|^2\end{pmatrix}</tex>$
1. Hallar el $<tex>Nu(T)</tex>$ y la $<tex>Im(T)</tex>$ .
2. Elegir una BOG 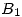$<tex>B_1</tex>$ y hallar $<tex>[T]_{B_1 B_2}</tex>$ siendo $<tex>B_2 = \left \{\begin{pmatrix} 1&0\\0&0\end{pmatrix},\begin{pmatrix} 0&1\\0&0\end{pmatrix},\begin{pmatrix} 0&0\\1&0\end{pmatrix},\begin{pmatrix} 0&0\\0&1\end{pmatrix}\right \}</tex>$ base de $<tex>\mathbf{R}^{2\times 2}</tex>$

Resolución

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.