Examen Parcial - 61.03. Algebra II -
Cátedra: Todas
Fecha: 2da Oportunidad - 2do Cuatrimestre 2011
Día: 12/11/2011
Enunciado
Punto I
Sea 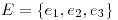 la base canónica de
la base canónica de 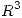 y sea
y sea 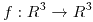 tal que
tal que 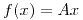 donde
donde 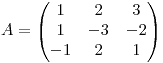 . ¿Existen isomorfismos lineales
. ¿Existen isomorfismos lineales 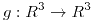 y
y 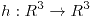 tales que
tales que ![<tex>[g o f o h]_{E,E}= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{pmatrix}</tex> <tex>[g o f o h]_{E,E}= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{pmatrix}</tex>](lib/plugins/latex/images/d4671f85fc2fade6f9d562fa9c4443be65d3f5cd_0.png) ? En caso afirmativo, calcular
? En caso afirmativo, calcular ![<tex>[g^{-1}]_{E,E}</tex> <tex>[g^{-1}]_{E,E}</tex>](lib/plugins/latex/images/eb6158d94f0dd7279d7cda0acf67d157bce93fcc_0.png) y
y ![<tex>[b]_{E,E}</tex> <tex>[b]_{E,E}</tex>](lib/plugins/latex/images/ec0583f6fe4bfd02fb2db44e7a1a92c34b4a1d62_0.png) para algunos de estos isomorfismos.
para algunos de estos isomorfismos.
Punto II
En 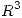 , consideramos el producto interno canónico. Dados
, consideramos el producto interno canónico. Dados ![<tex>x_{0}=[2,2,1]^t</tex> <tex>x_{0}=[2,2,1]^t</tex>](lib/plugins/latex/images/cb548dbe2d28463c2ae3655faa68ac8f32dd48e2_0.png) y
y 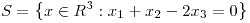 , encontrar, si existen, todos los
, encontrar, si existen, todos los 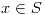 tales que:
tales que:

- El ángulo formado entre
 y
y 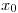 es
es 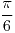
Punto III
Sea  el producto interno en el espacio
el producto interno en el espacio ![<tex> C^{6}[(-1,1],R] </tex> <tex> C^{6}[(-1,1],R] </tex>](lib/plugins/latex/images/32dfb231d7178dc9e554ad52647bb934969ddec3_0.png) dado por
dado por 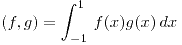 . Sea V el subespacio de
. Sea V el subespacio de ![<tex> C^{6}[(-1,1],R] </tex> <tex> C^{6}[(-1,1],R] </tex>](lib/plugins/latex/images/32dfb231d7178dc9e554ad52647bb934969ddec3_0.png) generado por
generado por 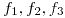 donde
donde 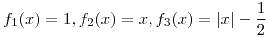 y sea
y sea 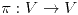 una proyección de rango 1 tal que
una proyección de rango 1 tal que  . Calcular la matriz de
. Calcular la matriz de  respecto de la base
respecto de la base 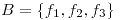 .
.
Punto IV
Sea 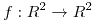 tal que
tal que 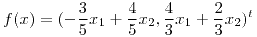 . Sabiendo que
. Sabiendo que  es la simetría respecto de cierto subespacio S de
es la simetría respecto de cierto subespacio S de 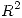 , encontrar todos los
, encontrar todos los 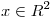 tales que
tales que 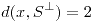 . (Considerar el producto interno canónico).
. (Considerar el producto interno canónico).
Punto V
Dada 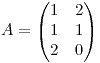 y dado
y dado 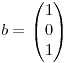 . Sean P y R las matrices de las proyecciones sobre el espacio columna de A y sobre el espacio fila de A, respectivamente. Encontrar todos los
. Sean P y R las matrices de las proyecciones sobre el espacio columna de A y sobre el espacio fila de A, respectivamente. Encontrar todos los 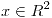 que hacen mínima la norma
que hacen mínima la norma 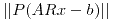 . ¿Cuál es el valor mínimo de esta norma? (Considerar el producto interno canónico).
. ¿Cuál es el valor mínimo de esta norma? (Considerar el producto interno canónico).
Resolución
