Examen Parcial - 61.08. Álgebra II A - 02/11/2009 - Tema 1
Enunciado
Ejercicio 1
Sea 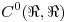 el espacio vectorial real de las funciones continuas
el espacio vectorial real de las funciones continuas 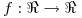 y sea
y sea 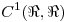 el espacio vectorial real de las funciones
el espacio vectorial real de las funciones 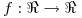 de clase
de clase 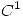 .
Compruebe que la aplicación
.
Compruebe que la aplicación 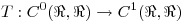 dada por
dada por 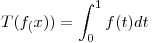 es una transformación lineal bien definida y encuentre una transformación lineal
es una transformación lineal bien definida y encuentre una transformación lineal 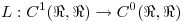 tal que
tal que 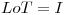 ( = identidad en
( = identidad en 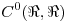 ). ¿Es
). ¿Es 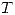 un isomorfismo lineal? ¿Es
un isomorfismo lineal? ¿Es 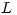 un isomorfismo lineal?
un isomorfismo lineal?
Ejercicio 2
Sea  un producto interno en
un producto interno en 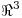 para el cual
para el cual 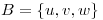 es una base ortonormal, donde
es una base ortonormal, donde 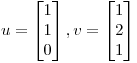 y
y 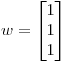 . Dado
. Dado 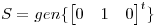 , hallar todos los elementos
, hallar todos los elementos 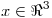 que verifican
que verifican 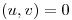 y además
y además 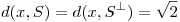 (donde la distancia es la asociada al producto interno dado).
(donde la distancia es la asociada al producto interno dado).
Ejercicio 3
Encontrar todas las matrices 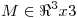 que verifican simultáneamente las siguientes tres condiciones: a)
que verifican simultáneamente las siguientes tres condiciones: a)  , b)
, b)  y c)
y c) 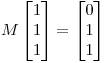
Ejercicio 4
Dada la matriz 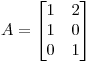 , hallar todos los
, hallar todos los 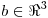 que verifican simultáneamente: (producto interno canónico): 1)
que verifican simultáneamente: (producto interno canónico): 1) 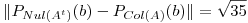 y 2) Para todo
y 2) Para todo 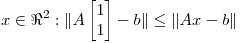 .
.
Ejercicio 5
Sea 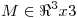 una matriz simétrica tal que
una matriz simétrica tal que 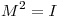 . Sabiendo que el subespacio
. Sabiendo que el subespacio 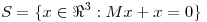 tiene dimensión 2 y que
tiene dimensión 2 y que 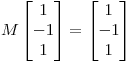 , calcular la matriz de la proyección (en
, calcular la matriz de la proyección (en 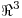 ) sobre
) sobre 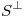 respecto de la base canónica. (Considere el producto interno canónico).
respecto de la base canónica. (Considere el producto interno canónico).
