Examen Parcial - 61.08. Álgebra II A - 31/10/2009 - Tema 1
Enunciado
Ejercicio 1:
Sea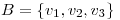 
una base de un espacio vectorial real 
, sea 
el subespacio de generado por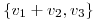 
y sea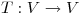 
una transformación lineal que verifica simultáneamente las siguientes tres condiciones:
a)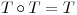 
b) 
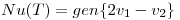y c)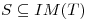 
Calcular ![<tex>[T]_{B,B}</tex>](lib/plugins/latex/images/685cc74c761c25dbbfe114ed5233bf040dfc1425_0.png "<tex>[T]_{B,B}</tex>")
. ¿Existe una única transformación lineal que verifique estas tres condiciones?
Ejercicio 2:
Determinar, si existen, todos los números reales 
para los cuales la fórmula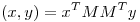 
define un producto interno en 
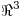, siendo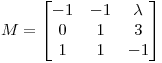 
Ejercicio 3:
Determinar todos los números reales para los cuales existe una matriz de proyección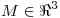 
(es decir: 
y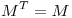 
) de rango 2 tal que 
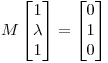. Para cada encontrado, exhibir una matriz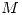 
que satisface estas condiciones.
Ejercicio 4:
Dad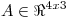a 
, sea 
la matriz de proyección en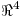 
sobre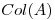 
respecto de la base canónica (y el producto interno canónico). Sabiendo que 
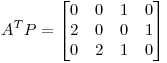resolver 
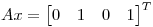por “cuadrados mínimos”.
Ejercicio 5:
Sea 
el producto interno en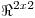 
dado por 
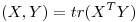. Calcule la distancia de la matriz identidad al subespacio ![<tex>S=gen \left[ \begin{bmatrix}{0}&{1}\\{1}&{1}\end{bmatrix} , \begin{bmatrix}{2}&{0}\\{0}&{1}\end{bmatrix} \right] </tex>](lib/plugins/latex/images/99c2533dcc5cde5c6c125706400c28910744ca05_0.png "<tex>S=gen \left[ \begin{bmatrix}{0}&{1}\\{1}&{1}\end{bmatrix} , \begin{bmatrix}{2}&{0}\\{0}&{1}\end{bmatrix} \right] </tex>")
.
