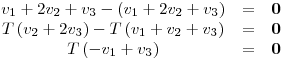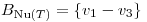Examen Parcial - 61.08. Álgebra II A - 27/10/2007
Cátedra: Indistinta
Fecha: 1° Oportunidad - 2° Cuatrimestre 2007
Día: 27/10/2007
Tema: 2
Enunciado
Punto I
- Demuestre que
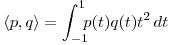 es producto interno en
es producto interno en  para todo
para todo  .
. - Considere en
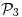 el p.i. definido en (a). Halle el elemento de de
el p.i. definido en (a). Halle el elemento de de 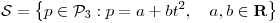 más cercano a
más cercano a  .
.
Punto II
- Sean
 y
y  matrices de proyección tales que
matrices de proyección tales que  .
.
Pruebe que es matriz de proyección. (Sugerencia: calcule primero
es matriz de proyección. (Sugerencia: calcule primero 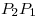 .)
.) - Hallar los
 que satisfagan simultáneamente:
que satisfagan simultáneamente: para todo
para todo  .
. ,
,
siendo![<tex>A= \left[ \begin{array}{lcr} 1 & 0 & 1 \\ 1 & 1 & 2 \\ 1 & -1 & 0 \end{array} \right]</tex> <tex>A= \left[ \begin{array}{lcr} 1 & 0 & 1 \\ 1 & 1 & 2 \\ 1 & -1 & 0 \end{array} \right]</tex>](lib/plugins/latex/images/062bddb59ded6fb421a09f244da5f71aadab58ef_0.png) y
y ![<tex>b=\left[ \begin{array}{c} 0 \\ 18 \\ 0 \end{array} \right]</tex> <tex>b=\left[ \begin{array}{c} 0 \\ 18 \\ 0 \end{array} \right]</tex>](lib/plugins/latex/images/f370c29a7a820a29eff8decc760ab8a852b1e903_0.png) .
.
Punto III
Sea 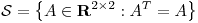 y sea
y sea 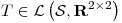 definida por
definida por 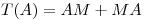 , con
, con ![<tex>M= \left[ \begin{array}{cc} 2 & 2 \\2 & 1\end{array} \right]</tex> <tex>M= \left[ \begin{array}{cc} 2 & 2 \\2 & 1\end{array} \right]</tex>](lib/plugins/latex/images/8f87d3df68195b404532e28c51e5cf25525791af_0.png) .
.
- Probar que
 es inyectiva, y que su imagen es
es inyectiva, y que su imagen es  .
. - Encontrar bases
 de
de  y
y  de
de  tales que
tales que ![<tex>[T]_{BC}</tex> <tex>[T]_{BC}</tex>](lib/plugins/latex/images/46b0ce084388c8de425928e8766dad26a05497e6_0.png) tenga unos en la diagonal principal y ceros en el resto.
tenga unos en la diagonal principal y ceros en el resto.
Punto IV
Sea 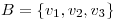 base de un
base de un  -espacio vectorial
-espacio vectorial  .
.
- ¿Para qué valores de
 existe
existe  tal que:
tal que:
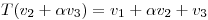
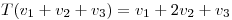
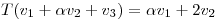 ?
?
¿para cuáles de ellos es T única? - Hallar, de entre los valores de
 para los cuales la transformación
para los cuales la transformación  del punto (a) es única, aquéllos que verifican la condición
del punto (a) es única, aquéllos que verifican la condición 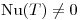 . Para tales valores hallar bases de
. Para tales valores hallar bases de  y de
y de  .
.
El examen se aprueba resolviendo correctamente cuatro puntos. Justificar todas las respuestas.
Resolución
Punto I

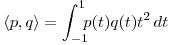 PI en
PI en 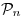 con
con  .
.
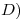
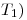

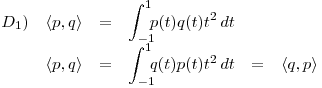
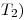
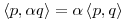
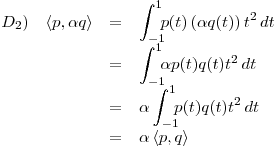
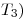
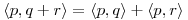
![<tex>\begin{array}{lrcl} D_3) & \left\langle p, q + r \right\rangle & = & \displaystyle \int_{-1}^1 \! \! \! p(t) \left[ q(t) + r(t) \right] t^2 \, dt \\ & & = & \displaystyle \int_{-1}^1 \! \! \! \left[ p(t) q(t) t^2 + p(t) r(t) t^2 \right] \, dt \\ & & = & \displaystyle \int_{-1}^1 \! \! \! p(t) q(t) t^2 \, dt + \int_{-1}^1 \! \! \! p(t) r(t) t^2 \, dt \\ & & = & \left\langle p,q \right\rangle + \left\langle p,r \right\rangle \end{array}</tex> <tex>\begin{array}{lrcl} D_3) & \left\langle p, q + r \right\rangle & = & \displaystyle \int_{-1}^1 \! \! \! p(t) \left[ q(t) + r(t) \right] t^2 \, dt \\ & & = & \displaystyle \int_{-1}^1 \! \! \! \left[ p(t) q(t) t^2 + p(t) r(t) t^2 \right] \, dt \\ & & = & \displaystyle \int_{-1}^1 \! \! \! p(t) q(t) t^2 \, dt + \int_{-1}^1 \! \! \! p(t) r(t) t^2 \, dt \\ & & = & \left\langle p,q \right\rangle + \left\langle p,r \right\rangle \end{array}</tex>](lib/plugins/latex/images/c989e7b25aa7e3d9b7a1bd761608f39ad3b603c1_0.png)
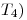
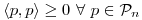
![<tex>\begin{array}{lccccc} D_4) & \left\langle p,p \right\rangle & = & \displaystyle \int_{-1}^1 \! \! \! {\left[ p(t) \right]}^2 t^2 \, dt & = & \displaystyle \int_{-1}^1 \! \! \! {\left[ p(t) t \right]}^2 \, dt\\ \end{array}</tex> <tex>\begin{array}{lccccc} D_4) & \left\langle p,p \right\rangle & = & \displaystyle \int_{-1}^1 \! \! \! {\left[ p(t) \right]}^2 t^2 \, dt & = & \displaystyle \int_{-1}^1 \! \! \! {\left[ p(t) t \right]}^2 \, dt\\ \end{array}</tex>](lib/plugins/latex/images/c4a91814f79f32b3f1076f26957ccaf1d8365e2f_0.png) .
.
Lo que aquí tenemos es la integral de una funcón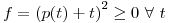 . Como la integral puede interpretarse geométricamente como el área bajo la curva que es gráfico de
. Como la integral puede interpretarse geométricamente como el área bajo la curva que es gráfico de  (si
(si 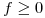 ), y como
), y como 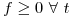 , se desprende que dicha área será positiva, y por lo tanto también la integral, y entonces:
, se desprende que dicha área será positiva, y por lo tanto también la integral, y entonces: 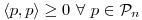 .
.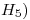

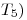
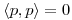
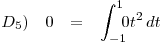
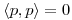

![<tex>\begin{array}{lccccccccc} D_6) & 0 = & \left\langle 0,0 \right\rangle & = & \displaystyle \int_{-1}^1 \! \! \! {\left[ p(t) t \right]}^2 \, dt \end{array}</tex> <tex>\begin{array}{lccccccccc} D_6) & 0 = & \left\langle 0,0 \right\rangle & = & \displaystyle \int_{-1}^1 \! \! \! {\left[ p(t) t \right]}^2 \, dt \end{array}</tex>](lib/plugins/latex/images/9e65aee0ac68f02f9e4c76687531762d971d9829_0.png) .
.
Llamando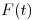 a la primitiva de
a la primitiva de 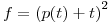 , es:
, es:
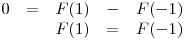 .
.
Por otro lado, sabemos que es siempre creciente (o, a lo sumo, constante), pues su derivada,
es siempre creciente (o, a lo sumo, constante), pues su derivada, 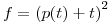 , es mayor o igual a cero para todo
, es mayor o igual a cero para todo  .
.
Es claro que en estas condiciones, debe ser constante, pues
constante, pues 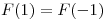 y
y 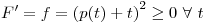 . Luego, si
. Luego, si
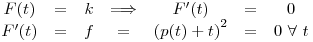 ,
,
y como no es cierto que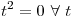 ,
,
debe ser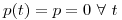
Por cumplirse las seis condiciones expuestas, queda probado que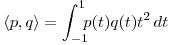 es producto interno en
es producto interno en 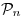 para todo
para todo  .
.
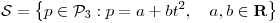 .
.
El elemento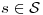 buscado es tal que
buscado es tal que
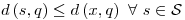
id est,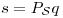 .
.
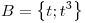 es base de
es base de  .
.
Con el método de Gram-Schmidt puedo hallar una BOG1) de  .
.
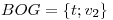 , donde
, donde
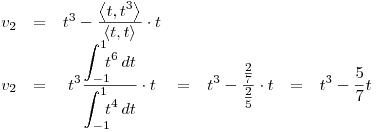
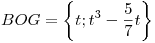
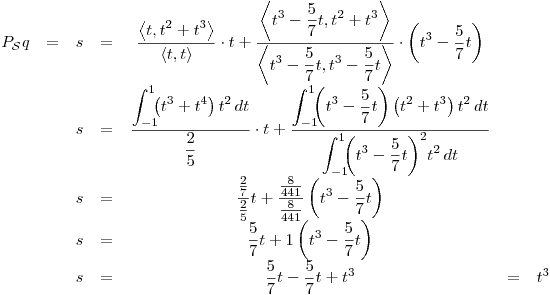
Punto II
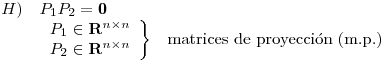
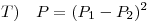 es matriz de proyección.
es matriz de proyección.
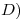 Para que
Para que  sea m.p. debe ser:
sea m.p. debe ser:
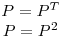
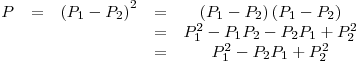
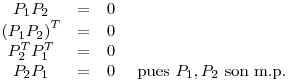
Entonces:
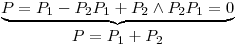
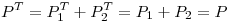
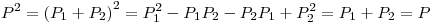
P es entonces matriz de proyección.- Debo hallar
 para todo
para todo  .
.
De (I) se deduce que  debe ser tal que la distancia de
debe ser tal que la distancia de 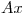 a
a  sea la menor posible, esto es:
sea la menor posible, esto es:
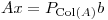
Por otro lado, de (II) tenemos que  debe ser CL de las filas de A:
debe ser CL de las filas de A:
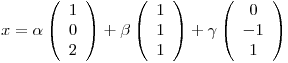
pero como 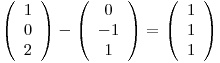
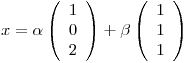
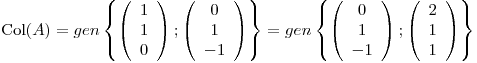
Casualmente, 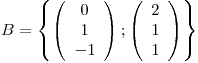 es BOG de
es BOG de 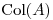 , considerando el PI canónico, con lo cual, llamando
, considerando el PI canónico, con lo cual, llamando 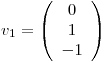 y
y 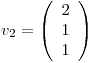 :
:
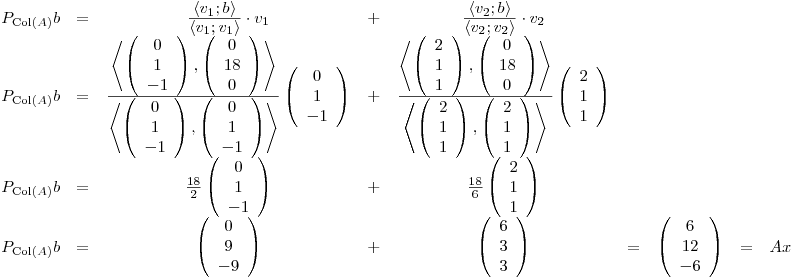
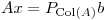
![<tex>\begin{array}{cccc} \left[ \begin{array}{ccc|c} 1 & 0 & 2 & 6 \\ 1 & 1 & 1 & 12 \\ 0 & -1 & 1 & -6 \end{array} \right] & \longrightarrow & \left[ \begin{array}{ccc|c} 1 & 0 & 2 & 6 \\ 0 & 1 & -1 & 6 \\ 0 & 0 & 0 & 0 \end{array} \right] & \begin{array}{c} x_2=x_3+6 \\ x_1=-2x_3+6 \end{array} \end{array}</tex> <tex>\begin{array}{cccc} \left[ \begin{array}{ccc|c} 1 & 0 & 2 & 6 \\ 1 & 1 & 1 & 12 \\ 0 & -1 & 1 & -6 \end{array} \right] & \longrightarrow & \left[ \begin{array}{ccc|c} 1 & 0 & 2 & 6 \\ 0 & 1 & -1 & 6 \\ 0 & 0 & 0 & 0 \end{array} \right] & \begin{array}{c} x_2=x_3+6 \\ x_1=-2x_3+6 \end{array} \end{array}</tex>](lib/plugins/latex/images/91605b7c076238a8924a6812142b982745948a46_0.png)
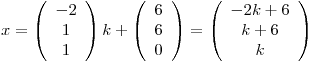
y como también:
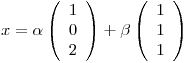
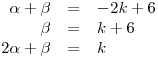
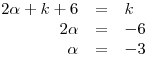
Como
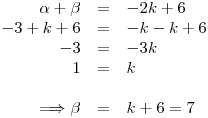
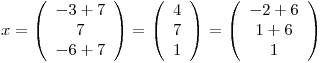
Punto III
a) 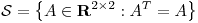
id est, si 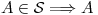 es simétrica.
es simétrica.
![<tex>T(A) = A \left[ \begin{array}{cc} 2 & 2 \\ 2 & 1 \end{array} \right] + \left[ \begin{array}{cc} 2 & 2 \\ 2 & 1 \end{array} \right] A, \ T \in \mathcal{L}\left( \mathcal{S}, \mathbf{R}^{2 \times 2} \right)</tex> <tex>T(A) = A \left[ \begin{array}{cc} 2 & 2 \\ 2 & 1 \end{array} \right] + \left[ \begin{array}{cc} 2 & 2 \\ 2 & 1 \end{array} \right] A, \ T \in \mathcal{L}\left( \mathcal{S}, \mathbf{R}^{2 \times 2} \right)</tex>](lib/plugins/latex/images/8e35f186be4e01a86e8992ba47c5c1c78d825430_0.png) .
.
Como 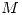 también es simétrica, id est,
también es simétrica, id est,
![<tex>M = \left[ \begin{array}{cc} 2 & 2 \\ 2 & 1 \end{array} \right] = M^T</tex> <tex>M = \left[ \begin{array}{cc} 2 & 2 \\ 2 & 1 \end{array} \right] = M^T</tex>](lib/plugins/latex/images/6bf649cb6369639e381f70174653662c88dd0bf9_0.png)
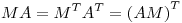
Supongamos que
![<tex>A = \left[ \begin{array}{cc} a_{11} & a_3 \\ a_3 & a_{22} \end{array} \right]</tex> <tex>A = \left[ \begin{array}{cc} a_{11} & a_3 \\ a_3 & a_{22} \end{array} \right]</tex>](lib/plugins/latex/images/e6e6c8475d9e93a24cedf2cfd36ba9f16160be23_0.png)
![<tex>AM = \left[ \begin{array}{cc} a_{11} & a_3 \\ a_3 & a_{22} \end{array} \right] \left[ \begin{array}{cc} 2 & 2 \\ 2 & 1 \end{array} \right] = \left[ \begin{array}{cc} 2a_{11}+2a_3 & 2a_{11}+a_3 \\ 2a_3+2a_{22} & 2a_3+a_{22} \end{array} \right]</tex> <tex>AM = \left[ \begin{array}{cc} a_{11} & a_3 \\ a_3 & a_{22} \end{array} \right] \left[ \begin{array}{cc} 2 & 2 \\ 2 & 1 \end{array} \right] = \left[ \begin{array}{cc} 2a_{11}+2a_3 & 2a_{11}+a_3 \\ 2a_3+2a_{22} & 2a_3+a_{22} \end{array} \right]</tex>](lib/plugins/latex/images/0d1604b9d1ed6dbef4ac4fde82f058a0cc1e2cc1_0.png)
![<tex>{\left( AM \right)}^T = \left[ \begin{array}{cc} 2a_{11}+2a_3 & 2a_3+2a_{22} \\ 2a_{11}+a_3 & 2a_3+a_{22} \end{array} \right]</tex> <tex>{\left( AM \right)}^T = \left[ \begin{array}{cc} 2a_{11}+2a_3 & 2a_3+2a_{22} \\ 2a_{11}+a_3 & 2a_3+a_{22} \end{array} \right]</tex>](lib/plugins/latex/images/bff3409f1435146345fdcf5d438909a5109a3023_0.png)
![<tex>T(A) = AM + {\left( AM \right)}^T = \left[ \begin{array}{cc} 4a_{11}+4a_3 & 2a_{11}+3a_3+2a_{22} \\ 2a_{11}+3a_3+2a_{22} & 4a_3+2a_{22} \end{array} \right]</tex> <tex>T(A) = AM + {\left( AM \right)}^T = \left[ \begin{array}{cc} 4a_{11}+4a_3 & 2a_{11}+3a_3+2a_{22} \\ 2a_{11}+3a_3+2a_{22} & 4a_3+2a_{22} \end{array} \right]</tex>](lib/plugins/latex/images/1a291ca2fe2be8c5177e43b17543b0077921b948_0.png)
Para 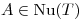 es:
es:
![<tex>\left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right] = T(A) \Longrightarrow \left\{ \begin{array}{ccl} 0 & = & 4a_{11} + 4a_3 \\ 0 & = & 4a_3+2a_{22} \\ 0 & = & 2a_{11}+3a_3+2a_{22}\end{array} \right.</tex> <tex>\left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right] = T(A) \Longrightarrow \left\{ \begin{array}{ccl} 0 & = & 4a_{11} + 4a_3 \\ 0 & = & 4a_3+2a_{22} \\ 0 & = & 2a_{11}+3a_3+2a_{22}\end{array} \right.</tex>](lib/plugins/latex/images/8d82cc91583325b09712f5e3e652289c8b9d227d_0.png)
![<tex>\left[ \begin{array}{ccc|c} 4 & 4 & 0 & 0 \\ 0 & 4 & 2 & 0 \\ 2 & 3 & 2 & 0 \end{array} \right] \longrightarrow \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right]</tex> <tex>\left[ \begin{array}{ccc|c} 4 & 4 & 0 & 0 \\ 0 & 4 & 2 & 0 \\ 2 & 3 & 2 & 0 \end{array} \right] \longrightarrow \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right]</tex>](lib/plugins/latex/images/feab56dbcd8c48e093cd62ccc35c28bb2d5b7270_0.png)
id est, 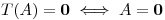
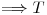 es inyectiva
es inyectiva
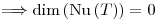
Como 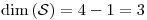 (finita)
(finita)

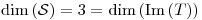
y como 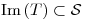
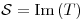
b)  base de
base de  ,
, 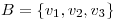
 base de
base de  ,
, 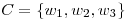
![<tex>{\left[ T \right]}_{BC} = \left[ \mathbf{C}_C \left( T \left( v_1 \right) \right) \quad \mathbf{C}_C \left( T \left( v_2 \right) \right) \quad \mathbf{C}_C \left( T \left( v_3 \right) \right) \right]</tex> <tex>{\left[ T \right]}_{BC} = \left[ \mathbf{C}_C \left( T \left( v_1 \right) \right) \quad \mathbf{C}_C \left( T \left( v_2 \right) \right) \quad \mathbf{C}_C \left( T \left( v_3 \right) \right) \right]</tex>](lib/plugins/latex/images/871c6d700eda69673071e7339b6fc98ce4efb13c_0.png)
Como  tiene tres elementos y
tiene tres elementos y  tiene cuatro elementos,
tiene cuatro elementos, 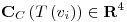 , y entonces
, y entonces ![<tex>{\left[ T \right]}_{BC} \in \mathbf{R}^{4 \times 3}</tex> <tex>{\left[ T \right]}_{BC} \in \mathbf{R}^{4 \times 3}</tex>](lib/plugins/latex/images/7d63aaccd16448f266eedb8d1fa3dd1fddcee09b_0.png)
![<tex>{\left[ T \right]}_{BC} = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array} \right]</tex> <tex>{\left[ T \right]}_{BC} = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array} \right]</tex>](lib/plugins/latex/images/36b25712260aab27104032392056cc620979753b_0.png) , que la última fila de
, que la última fila de ![<tex>{\left[ T \right]}_{BC}</tex> <tex>{\left[ T \right]}_{BC}</tex>](lib/plugins/latex/images/20d6bafc9a3cca9baf0a50960f22f47fbb5228c9_0.png) sea
sea 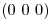 implica que
implica que 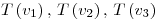 son LI con
son LI con 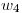 .
.
Por otro lado, si 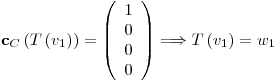 y así con el resto:
y así con el resto: 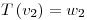 y
y 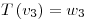
Elijo pues la base ![<tex>B=\left\{ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right], \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right], \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right] \right\}</tex> <tex>B=\left\{ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right], \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right], \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right] \right\}</tex>](lib/plugins/latex/images/bbc24033036db2ef2e8b13f407686a30cb462f76_0.png)
![<tex>\begin{array}{cl} \left. \begin{array}{ccccccc} T \left( v_1 \right) & = & T \left( \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right] \right) & = & \left[ \begin{array}{cc} 4 & 2 \\ 2 & 0 \end{array} \right] & = & w_1\\T \left( v_2 \right) & = & T \left( \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right] \right) & = & \left[ \begin{array}{cc} 4 & 3 \\ 3 & 4 \end{array} \right] & = & w_2\\ T \left( v_3 \right) & = & T \left( \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right] \right) & = & \left[ \begin{array}{cc} 0 & 2 \\ 2 & 2 \end{array} \right] & = & w_3\\ \end{array} \right\} & \mbox{son LI, lo cual es coherente pues }B\mbox{ es base y pues }\dim \left( \mathrm{Im}\left(T \right) \right) = 3 \end{array}</tex> <tex>\begin{array}{cl} \left. \begin{array}{ccccccc} T \left( v_1 \right) & = & T \left( \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right] \right) & = & \left[ \begin{array}{cc} 4 & 2 \\ 2 & 0 \end{array} \right] & = & w_1\\T \left( v_2 \right) & = & T \left( \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right] \right) & = & \left[ \begin{array}{cc} 4 & 3 \\ 3 & 4 \end{array} \right] & = & w_2\\ T \left( v_3 \right) & = & T \left( \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right] \right) & = & \left[ \begin{array}{cc} 0 & 2 \\ 2 & 2 \end{array} \right] & = & w_3\\ \end{array} \right\} & \mbox{son LI, lo cual es coherente pues }B\mbox{ es base y pues }\dim \left( \mathrm{Im}\left(T \right) \right) = 3 \end{array}</tex>](lib/plugins/latex/images/cecbab360bb0d24106b97e61d3130ab3bc2aee6c_0.png)
Ahora propongo  , id est,
, id est, 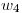 no simétrico:
no simétrico: ![<tex>w_4 = \left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right]</tex> <tex>w_4 = \left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right]</tex>](lib/plugins/latex/images/ae4f5e0a9dec9b70b2eb3aa4f3c77abaa2691e30_0.png)
![<tex>B=\left\{ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right], \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right], \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right] \right\}</tex> <tex>B=\left\{ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right], \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right], \left[ \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right] \right\}</tex>](lib/plugins/latex/images/bbc24033036db2ef2e8b13f407686a30cb462f76_0.png)
![<tex>C=\left\{ \left[ \begin{array}{cc} 4 & 2 \\ 2 & 0 \end{array} \right], \left[ \begin{array}{cc} 4 & 3 \\ 3 & 4 \end{array} \right], \left[ \begin{array}{cc} 0 & 2 \\ 2 & 2 \end{array} \right], \left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right] \right\}</tex> <tex>C=\left\{ \left[ \begin{array}{cc} 4 & 2 \\ 2 & 0 \end{array} \right], \left[ \begin{array}{cc} 4 & 3 \\ 3 & 4 \end{array} \right], \left[ \begin{array}{cc} 0 & 2 \\ 2 & 2 \end{array} \right], \left[ \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right] \right\}</tex>](lib/plugins/latex/images/7b67e3453ca47ac2b657a97fc9d8b0bdd0b46a1d_0.png)
Punto IV
a) 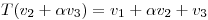
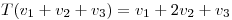
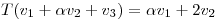
Si  :
:
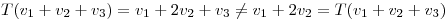
Lo cual es claramente un absurdo pues  debe asignar un solo elemento del espacio de llegada a cada elemento del espacio de partida.
debe asignar un solo elemento del espacio de llegada a cada elemento del espacio de partida.
Un absurdo así no podría ocurrir, por otro lado, en el caso de:
 y
y 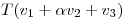
pues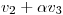 es LI con
es LI con 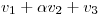 independientemente de
independientemente de  .
. y
y 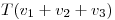 pues
pues 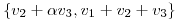 LI
LI 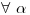 .
.
Por otro lado, claramente se ve que, independientemente del  considerado,
considerado,  será lineal.
será lineal.
 existe, pues, para
existe, pues, para 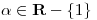 .
.
Para que  sea única es condición necesaria y suficiente que
sea única es condición necesaria y suficiente que  sea base de
sea base de  . Para ello los tres elementos (y por ende sus coordenadas en base
. Para ello los tres elementos (y por ende sus coordenadas en base  ) deben ser LI.
) deben ser LI.
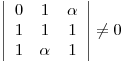
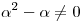
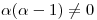
 es única para
es única para 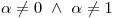
b) Para que 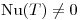 deben ser los generadores de
deben ser los generadores de  LD, id est,
LD, id est,
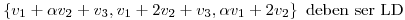
Ello ocurre si y sólo si
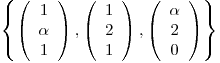 (sus coordenadas en base
(sus coordenadas en base  ) lo son.
) lo son.
Para encontrar los valores de  que satisfacen la susodicha condición, hallo el determinante:
que satisfacen la susodicha condición, hallo el determinante:
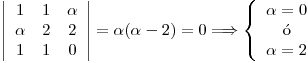
Elijo  pues así garantizo la existencia y unicidad de
pues así garantizo la existencia y unicidad de  y simultáneamente, la condición de que
y simultáneamente, la condición de que 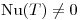 .
.
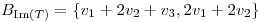
Por otro lado: