Examen Parcial - 61.08. Álgebra II A - 27/10/2007
- Enunciado
  - Punto I
  - Punto II
  - Punto III
  - Punto IV
- Resolución
  - Punto I
  - Punto II
  - Punto III
  - Punto IV
- Discusión

2007

Cátedra: Indistinta
Fecha: 1° Oportunidad - 2° Cuatrimestre 2007
Día: 27/10/2007

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Punto I

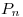Demuestre que $<tex>(p,q)=\int_{-1}^1 p(t)q(t) t^2 \, dt</tex>$ es un producto interno en $<tex>P_n</tex>$ para todo $<tex>n \in \mathbf{N}_0</tex>$ .
Con el PI de (1), hallar el elemento de $<tex>S=\left\{ p \in P_3: p=a+bt^2, \quad a,b \in \mathbf{R} \right\}</tex>$ más cercano a $<tex>q=t^2+t^3</tex>$ .

Punto II

$<tex>P_1 \in \mathbf{R}^{n \times n}</tex>$ es una matriz de proyección, $<tex>P_2 \in \mathbf{R}^{nxn}</tex>$ es una matriz de proyección, $<tex>P_1P_2=0</tex>$ .
Demostrar que $<tex>P=(P_1-P_2)^2</tex>$ es una matriz de proyección.

(Sugerencia: calcular primero 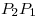$<tex>P_2P_1</tex>$ .)

Hallar los $<tex>x \in \mathbf{R}^3</tex>$ que cumplan con las siguientes condiciones:
1. $<tex> \left\| Ax-b \right\| \leq \left\| Az-b \right\|</tex>$ para todo $<tex>z \in \mathbf{R}^3</tex>$ .
2. $<tex>x \in \mathrm{Fil}(A)</tex>$ ,
  $<tex>A= \left[ \begin{array}{lcr} 1 & 0 & 1 \\ 1 & 1 & 2 \\ 1 & -1 & 0 \end{array} \right]</tex>$ .

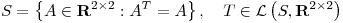$<tex>S=\left\{ A \in \mathbf{R}^{2\times 2}:A^T=A \right\}, \quad T \in \mathcal{L}\left( S,\mathbf{R}^{2\times 2} \right)</tex>$ tal que $<tex>T(A)=AM+MA,\quad M= \left[ \begin{array}{cc}1 & 2 \\2 & 2\end{array} \right]</tex>$ .

Demostrar que $<tex>T</tex>$ es inyectiva, y que $<tex>\mathrm{Im}(T)=S</tex>$ .
Encontrar bases $<tex>B</tex>$ de $<tex>S</tex>$ y $<tex>C</tex>$ de $<tex>\mathbf{R}^{2 \times 2}</tex>$ tal que $<tex>[T]_{BC}</tex>$ tenga unos en la diagonal principal y ceros en los lugares restantes.

Punto IV

$<tex> B=\{v_1,v_2,v_3\}</tex>$ base de $<tex>V</tex>$ , buscar para cuales $<tex>\alpha \in \mathbf{R}</tex>$ existe $<tex>T \in \mathcal{L}(V)</tex>$ tal que:
$<tex>T(v_1+ \alpha v_2)=\alpha v_1+v_2+v_3</tex>$
$<tex>T(v_1+v_2+v_3)=2v_1+v_2+v_3</tex>$
$<tex>T(v_1+ \alpha v_2)=2V_1+ \alpha v_3</tex>$
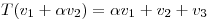
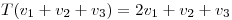
y encontrar para cuales valores de $<tex>\alpha</tex>$ la TL es única.
de entre los valores de $<tex>\alpha</tex>$ hallados en (1) para los cuales la TL es única, encontrar los $<tex>\alpha</tex>$ para los cuales $<tex>\mathrm{Nu}(T)\not=0</tex>$ . Para los valores hallados encontrar bases de $<tex>\mathrm{Nu}(T)</tex>$ e $<tex>\mathrm{Im}(T)</tex>$ .

Resolución

Punto I

Punto II

Punto III

Punto IV

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.