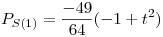Parcial Algebra II 1ra fecha (12/5/2007)
1)
a) Probar que existe único Pi en P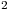 tal que:
tal que:
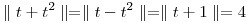 ;
;
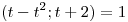 ;
;
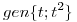
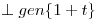
b) Considerado el Pi de (a) hallar elemento 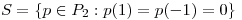 más cercano a
más cercano a 
2) a) Sea 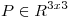 una matriz de proyección tal que:
una matriz de proyección tal que:
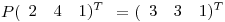 y
y 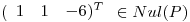
Hallar  y el subespacio sobre el cual proyecta.
y el subespacio sobre el cual proyecta.
b) Sea 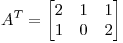
sabiendo que ||Ax-b||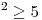 para
para 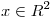 y que ||Az-b||
y que ||Az-b|| si
si
![<tex>z=\left[ 1-t\right]^{T} </tex> <tex>z=\left[ 1-t\right]^{T} </tex>](lib/plugins/latex/images/bcfa63660fb028f42a81ee579fa4ee1ea05dd8ac_0.png)
hallar los posibles valores de 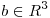
3) a) Hallar los valores de 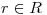 para los cuales existe una única
para los cuales existe una única
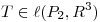 que verifica:
que verifica:
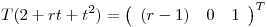
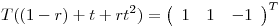
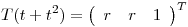
Hallar bases de  y de
y de  en los casos en que
en los casos en que  no es
inyectiva.
no es
inyectiva.
b) Entre los valores de  hallados en (a) encuentre aquellos
para los cuales existen bases B de
hallados en (a) encuentre aquellos
para los cuales existen bases B de  y C de R
y C de R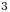 tales que:
tales que:
![<tex>\left[ T\right]_{BC}=\begin{bmatrix}2 & 0 & 0 \\0 &-1 & 0\\0 & 0 &0 \\\end{bmatrix}</tex> <tex>\left[ T\right]_{BC}=\begin{bmatrix}2 & 0 & 0 \\0 &-1 & 0\\0 & 0 &0 \\\end{bmatrix}</tex>](lib/plugins/latex/images/7872cda5f52225ec279f90237de692d9403e7915_0.png) . (Exhiba tales bases)
. (Exhiba tales bases)
4) Sea 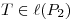 definida por:
definida por: ![<tex>T(p)=(1+t)\left[ (2p(t)-tp^{'}(t)+p^{''}(t)\right] </tex> <tex>T(p)=(1+t)\left[ (2p(t)-tp^{'}(t)+p^{''}(t)\right] </tex>](lib/plugins/latex/images/6e3dfcd554c5817e13d271085e0a5eb13a715d79_0.png)
a) Hallar los posibles valores de 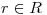 para los cuales
para los cuales 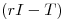 no es inversible.
no es inversible.
b) Definir 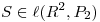 y
y
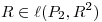 tales que
tales que 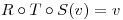 para todo
para todo 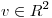
RESOLUCION:
Ejercicio 2:
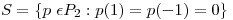
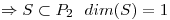
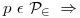
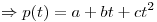
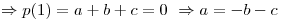
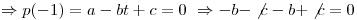
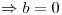
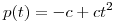
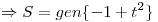
El elemento más cercano a  es
es 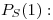
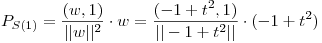
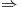 Con el PI definido:
Con el PI definido:
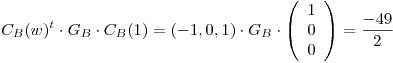
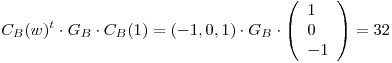
Finalmente: