Examen (Parcial) - 61.08. Álgebra - 13/12/2006
Catedra: Todas
Fecha: 2º Oportunidad - 2º Cuatrimestre 2006
Día: 13/12/2006
Tema: 2
Enunciado
1
(a) Probar que 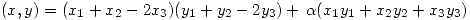 es producto interno en
es producto interno en 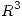 si y sólo si
si y sólo si 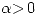
(b) Considerando el p.i. definido en (a) con  hallar todos los
hallar todos los 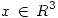 cuya distancia al subespacio
cuya distancia al subespacio 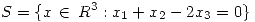 sea 1.
sea 1.
2
(a) Hallar 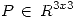 , sabiendo que P es de proyección y que
, sabiendo que P es de proyección y que ![<tex>(I - P) \left[ \begin{array}{rr} 6 & 6 \\ -6 & 6 \\ 0 &6 \\\end{array} \right] = \left[ \begin{array}{cc} 3 & 13 \\ 0 & 4 \\ 3 & 5\\ \end{array} \right] </tex> <tex>(I - P) \left[ \begin{array}{rr} 6 & 6 \\ -6 & 6 \\ 0 &6 \\\end{array} \right] = \left[ \begin{array}{cc} 3 & 13 \\ 0 & 4 \\ 3 & 5\\ \end{array} \right] </tex>](lib/plugins/latex/images/f5390874b971176c3496b11d180270609948a91a_0.png)
(b) Sean 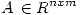 y
y 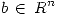 . Decidir, justificando la respuesta, si las siguientes afirmaciones son verdaderas o falsas
. Decidir, justificando la respuesta, si las siguientes afirmaciones son verdaderas o falsas
(i) Si el rango(A) 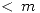 , entonces la ecuación
, entonces la ecuación 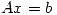 tiene infinitas soluciones por cuadrados mínimos.
tiene infinitas soluciones por cuadrados mínimos.
(ii) Si 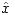 es una solución por cuadrados mínimos de la ecuación
es una solución por cuadrados mínimos de la ecuación 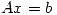 y
y 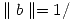 , entonces
, entonces 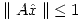
3) Sea 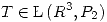 tal que, para ciertos
tal que, para ciertos ![<tex>\alpha , \beta \in R,\; T([1 \; 1 \; 0]^t) = \beta + (\alpha - 2)t^2, \; T([0 \; 1 \; 1]^t) = \beta t + \alpha t^2, \;</tex> <tex>\alpha , \beta \in R,\; T([1 \; 1 \; 0]^t) = \beta + (\alpha - 2)t^2, \; T([0 \; 1 \; 1]^t) = \beta t + \alpha t^2, \;</tex>](lib/plugins/latex/images/2923270800970ef4596e27b9539f8cdcfd556e6b_0.png)
![<tex> T([0 \; 0 \; 1]^t) = 2 \beta + \alpha t^2. </tex> <tex> T([0 \; 0 \; 1]^t) = 2 \beta + \alpha t^2. </tex>](lib/plugins/latex/images/05ec7cead9ccb7564d3592575a6062c30ddc8854_0.png)
(a) Determinar para qué valores de 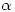 y
y 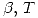 no es inyectiva. Para los valores de
no es inyectiva. Para los valores de 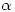 y
y 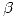 hallados que cumplan la condición
hallados que cumplan la condición 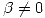 , hallar bases del núcleo y de la imagen de
, hallar bases del núcleo y de la imagen de  .
.
(b) Considerando  y
y 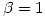 , justificar la existencia de
, justificar la existencia de 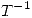 y calcular
y calcular 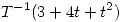 .
.
4) Considere la ecuación diferencial: 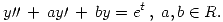
(a) Sabiendo que 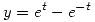 es solución de la ecuación homogénea asociada, hallar
es solución de la ecuación homogénea asociada, hallar  y
y  y exhibir una base de soluciones de tal ecuación.
y exhibir una base de soluciones de tal ecuación.
(b) Considerando los valores de  y
y  obtenidos en (a), encuentre todas las soluciones de la ecuación no homogénea que verifican
obtenidos en (a), encuentre todas las soluciones de la ecuación no homogénea que verifican 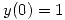 y
y 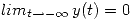
El examen se aprueba resolviendo correctamente cuatro puntos. Justificar todas las respuestas.
Resolución
