Examen Parcial - 61.08. Álgebra II A - 14 de Diciembre de 2005
Cátedra: Indistinta
Fecha: 3° Oportunidad - 2° Cuatrimestre 2005
Día: 14/12/2005
Tema: 1.
Enunciado
Punto I
a)
Sea 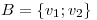 base de un
base de un  -espacio vectorial
-espacio vectorial  . Definir un producto interno en
. Definir un producto interno en  que verifique simultáneamente:
que verifique simultáneamente:
i) 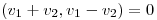
ii) 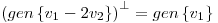
iii) 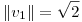 .
.
b)
Sea 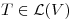 , definida por
, definida por 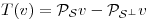 , donde
, donde 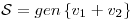 y el producto interno que se considera es el hallado en (a). Probar que para todo
y el producto interno que se considera es el hallado en (a). Probar que para todo 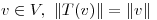 y hallar
y hallar ![<tex>[T]_B</tex> <tex>[T]_B</tex>](lib/plugins/latex/images/77974c5d33422dda29ab8c19452e9cbe246a3fa1_0.png) .
.
Punto II
a)
Sean 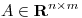 y
y 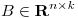 tales que
tales que 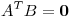 . Probar que
. Probar que  .
.
b)
Sean 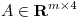 y
y 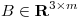 tales que
tales que 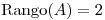 y
y ![<tex>BA= \left[ \begin{array}{rrrr} 1 & 1 & 1 & 0\\ 2 & 0 & 2 & 1\\ 1 & 1 & 1 & 0 \end{array} \right]</tex> <tex>BA= \left[ \begin{array}{rrrr} 1 & 1 & 1 & 0\\ 2 & 0 & 2 & 1\\ 1 & 1 & 1 & 0 \end{array} \right]</tex>](lib/plugins/latex/images/c8d9ff5784977bc8eb2c0d657c47cb5b4d017771_0.png) . Hallar la matriz de proyección sobre
. Hallar la matriz de proyección sobre 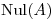 .
.
Punto III
Sea 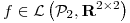 tal que
tal que ![<tex>[f]_{BB'} = \left[ \begin{array}{rrr} \alpha & 1 & \alpha +1\\ \alpha & 1 & 0\\ 2\alpha & 2\alpha & \alpha \end{array} \right]</tex> <tex>[f]_{BB'} = \left[ \begin{array}{rrr} \alpha & 1 & \alpha +1\\ \alpha & 1 & 0\\ 2\alpha & 2\alpha & \alpha \end{array} \right]</tex>](lib/plugins/latex/images/4c05f437245cb83de9e69076834f75742f1db141_0.png) , con
, con 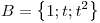 y
y 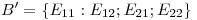 con
con 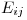 la matriz cuayas componentes son nulas salvo la de la posición
la matriz cuayas componentes son nulas salvo la de la posición 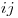 que es 1.
que es 1.
a)
Hallar los valores de  para los que existen
para los que existen 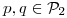 con
con 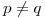 y
y ![<tex>f(p) = f(q) = \left[ \begin{array}{cc} 0 & 0\\ \alpha -1 & 2\alpha-2 \end{array} \right]</tex> <tex>f(p) = f(q) = \left[ \begin{array}{cc} 0 & 0\\ \alpha -1 & 2\alpha-2 \end{array} \right]</tex>](lib/plugins/latex/images/d0a5d5d9e4e299f3cd4fe2a0768313b39e93f16f_0.png) .
.
b)
Para  , hallar un subespacio
, hallar un subespacio  de
de 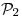 tal que la suma de
tal que la suma de  con
con 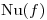 sea directa y
sea directa y 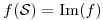 .
.
Punto IV
a)
Sea 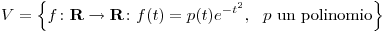 y, para
y, para  , sea
, sea 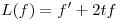 . Probar que
. Probar que 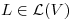 y que es sobreyectiva. Hallar
y que es sobreyectiva. Hallar 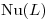 .
.
b)
Hallar todas las soluciones de 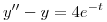 que verifiquen
que verifiquen 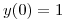 y
y 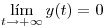 .
.
El examen se aprueba resolviendo correctamente cuatro puntos. Justificar todas las respuestas.
Resolución
