Examen Parcial - 61.08. Álgebra II A - 19 de Noviembre de 2005
Cátedra: Indistinta
Fecha: 3° Oportunidad - 2° Cuatrimestre 2005
Día: 19/11/2005.
Tema: 2.
Enunciado
Punto I
Sea  un
un  -espacio vectorial de dimensión 2 con producto interno
-espacio vectorial de dimensión 2 con producto interno 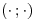 . Sean
. Sean  y
y  en
en  tales que
tales que 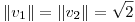 y
y 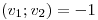 y sea
y sea 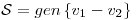 .
.
a)
Probar que 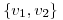 es base de
es base de  y hallar
y hallar 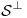 .
.
b)
Hallar todos los  cuya distancia a
cuya distancia a  es
es 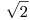 .
.
Punto II
a)
Sea 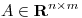 . Probar que si
. Probar que si  y
y  son, respectivamente, las matrices de proyección a
son, respectivamente, las matrices de proyección a 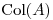 y a
y a 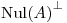 , entonces
, entonces 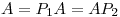 .
.
b)
Considere el sistema  , con
, con 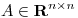 y
y 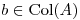 . Probar que existe un único
. Probar que existe un único 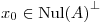 tal que
tal que 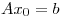 .
.
Punto III
Sea 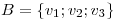 una base de
una base de  .
.
a)
Determinar todos los valores de 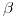 para los que existe una única
para los que existe una única 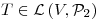 que verifique
que verifique 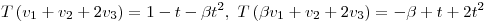 y
y 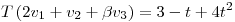 . Para esos valores de
. Para esos valores de 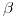 hallar bases de
hallar bases de  e
e  .
.
b)
Hallar entre los valores de 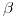 encontrados en (a), aquellos para los cuales la ecuación
encontrados en (a), aquellos para los cuales la ecuación 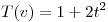 admite más de una solución.
admite más de una solución.
Punto IV
a)
Sea 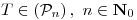 , definida por
, definida por 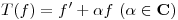 . Probar que
. Probar que  es biyectiva si y sólo si
es biyectiva si y sólo si 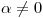 . Para
. Para  y
y  , hallar la representación matricial de
, hallar la representación matricial de  en la base
en la base 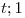 .
.
b)
Hallar la solución general de la ecuación 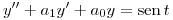 sabiendo que
sabiendo que 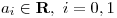 y que
y que 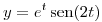 es solución general de la ecuación homogénea asociada.
es solución general de la ecuación homogénea asociada.
El examen se aprueba resolviendo correctamente cuatro puntos. Justificar todas las respuestas.
Resolución
