Examen Parcial - 61.08. Álgebra II A - 29 de Octubre de 2005
Cátedra: Indistinta
Fecha: 1° Oportunidad - 2° Cuatrimestre 2005
Día: 29/10/2005
Tema: 2.
Enunciado
Punto I
a)
Demostrar que 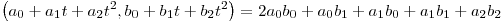 es producto interno en
es producto interno en 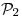 .
.
b)
Sean 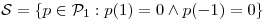 y
y  . Hallar todos los
. Hallar todos los 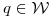 tales que
tales que 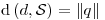 , considerando el PI definido en (a).
, considerando el PI definido en (a).
Punto II
a)
Sean 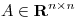 una matriz de proyección y
una matriz de proyección y  . Probar que si
. Probar que si  es solución por cuadrados mínimos de
es solución por cuadrados mínimos de  entonces
entonces 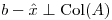 .
.
b)
Sea 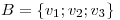 base de un espacio vectorial
base de un espacio vectorial  y sea
y sea 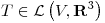 definida por
definida por 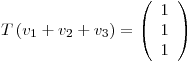 ,
, 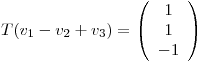 ,
, 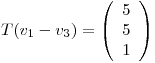 . Justificar la existencia y unicidad de
. Justificar la existencia y unicidad de  hallar todos los
hallar todos los  que minimizan
que minimizan 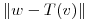 con
con 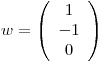 . (Considere el PI canónico en
. (Considere el PI canónico en 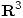 ).
).
Punto III
Sea 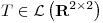 definida por
definida por 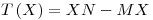 con
con ![<tex>N= \left[ \begin{array}{rr} 0 & 0\\ 0 & 1 \end{array} \right]</tex> <tex>N= \left[ \begin{array}{rr} 0 & 0\\ 0 & 1 \end{array} \right]</tex>](lib/plugins/latex/images/ba5ccef85f865c4065719487e77ad5b32c51010c_0.png) y
y ![<tex>M = \left[ \begin{array}{rr} \alpha & -1\\ -1 & \alpha \end{array} \right]</tex> <tex>M = \left[ \begin{array}{rr} \alpha & -1\\ -1 & \alpha \end{array} \right]</tex>](lib/plugins/latex/images/058778b92807223486b12ad31d1c34e8f3a10727_0.png) .
.
a)
Hallar todos los valores de  para los cuales
para los cuales  es biyectiva.
es biyectiva.
b)
Considerando 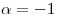 , defina transformaciones lineales
, defina transformaciones lineales 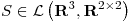 y
y 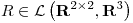 tales que
tales que 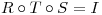 donde
donde 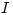 es la transformación identidad en
es la transformación identidad en 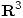
Punto IV
a)
Resolver el problema a valor inicial 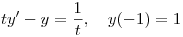 .
.
b)
Hallar la solución general de la ecuación 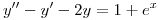
El examen se aprueba resolviendo correctamente cuatro puntos. Justificar todas las respuestas.
Resolución
