Parcial - 61.08. Álgebra II A
Cátedra: Todas
Fecha: 2da Oportunidad - 1er Cuatrimestre 2005
Día: 04/06/2005
Tema:1
Enunciado
- Demostrar que
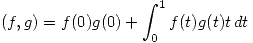 es producto interno en
es producto interno en 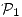 .
. - Hallar, considerando el p.i. definido en (I), todos los
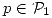 cuya distancia a
cuya distancia a 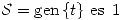 .
.
- Sea
![<tex> A = \left[ \begin{array}{lll} 1 & 0 & \ \ 1 \\ & \\1 & 0 & -1\\ & \\1 & 1 & \ \ 0 \\\end{array} \right] </tex> <tex> A = \left[ \begin{array}{lll} 1 & 0 & \ \ 1 \\ & \\1 & 0 & -1\\ & \\1 & 1 & \ \ 0 \\\end{array} \right] </tex>](lib/plugins/latex/images/8effd81da8fa95378973a401c6c6de145e2af869_0.png) Hallar matrices cuadradas
Hallar matrices cuadradas  y
y  ,
,  triangular inferior y
triangular inferior y  de filas ortonormales, tales que
de filas ortonormales, tales que 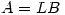 . (Sugerencia: considere
. (Sugerencia: considere 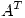 .)
.) - Sea
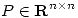 matriz de proyección y sea
matriz de proyección y sea 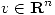 no nulo tal que
no nulo tal que 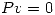 . Probar que
. Probar que 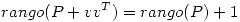 .
.
- Sea
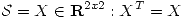 y sea
y sea 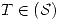 , definida por
, definida por 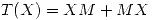 con
con 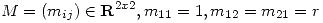 y
y 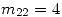 . Hallar todos los valores de
. Hallar todos los valores de  para los cuales
para los cuales  resulta biyectiva.
resulta biyectiva. - Determinar los valores de
 positivos para los cuales existen bases
positivos para los cuales existen bases  y e de
y e de  tales que
tales que ![<tex> [T]_{BC} = \left[ \begin{array}{lll} 1 & 1 & 0 \\ & \\0 & 1 & 0\\ & \\0 & 0 & 0 \\\end{array} \right] </tex> <tex> [T]_{BC} = \left[ \begin{array}{lll} 1 & 1 & 0 \\ & \\0 & 1 & 0\\ & \\0 & 0 & 0 \\\end{array} \right] </tex>](lib/plugins/latex/images/b30f94a6616688f70139afc72400fad9201ce246_0.png) Hallar tales bases.
Hallar tales bases.
- Sea
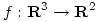 tal que para
tal que para 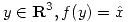 siendo
siendo  la solución por cuadrados mínimos de la ecuación
la solución por cuadrados mínimos de la ecuación
![<tex>Ax = y \mbox{ con } A^T = \left[ \begin{array}{lll} 1 & 1 & -1 \\ & \\1 & 0 & \ \ 1 \\\end{array} \right] </tex> <tex>Ax = y \mbox{ con } A^T = \left[ \begin{array}{lll} 1 & 1 & -1 \\ & \\1 & 0 & \ \ 1 \\\end{array} \right] </tex>](lib/plugins/latex/images/b7341d918f89bf879db8691cd2d62c99961ecdcb_0.png)
- Pruebe que
 es lineal y halle la representación matricial de
es lineal y halle la representación matricial de  en las bases canónicas.
en las bases canónicas. - Hallar núcleo e imagen de
 ·
·
Resolución
Punto 1
(I)
Para que 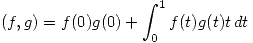 sea producto interno en
sea producto interno en 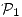 se deben cumplir las cuatro propiedades de p.i. Para ello se plantea lo siguiente:
se deben cumplir las cuatro propiedades de p.i. Para ello se plantea lo siguiente:
Sea
1. 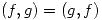
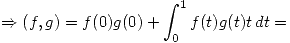
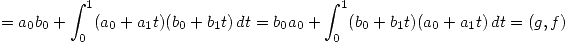
2. 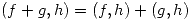
![<tex>\Rightarrow (f+g)(0)h(0) + \int_{0}^{1} (f+g)(t)h(t)t \, dt = [f(0)+g(0)]h(0) + \int_{0}^{1} [f(t)+g(t)]h(t)t \, dt =</tex> <tex>\Rightarrow (f+g)(0)h(0) + \int_{0}^{1} (f+g)(t)h(t)t \, dt = [f(0)+g(0)]h(0) + \int_{0}^{1} [f(t)+g(t)]h(t)t \, dt =</tex>](lib/plugins/latex/images/fe7f9129855fe1b9b387992bdcc4d6b4bd765b4a_0.png)
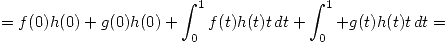
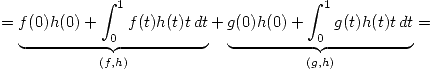
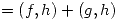
3.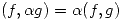
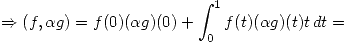
![<tex> = f(0) \alpha g(0) + \int_{0}^{1} f(t)\alpha g(t)t \, dt =\alpha [f(0) + g(0) + \int_{0}^{1} f(t)g(t)t \, dt] = \alpha (f,g)</tex> <tex> = f(0) \alpha g(0) + \int_{0}^{1} f(t)\alpha g(t)t \, dt =\alpha [f(0) + g(0) + \int_{0}^{1} f(t)g(t)t \, dt] = \alpha (f,g)</tex>](lib/plugins/latex/images/cfb4350cd5d7fce619af765d46d632ea5c43376d_0.png)
4. 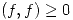 ,
, 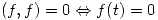
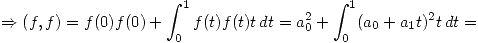
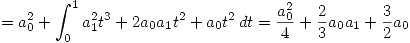
Se cuentan cuadrados:
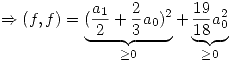
Para que 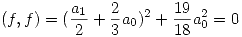 se tiene que cumplir que
se tiene que cumplir que 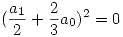 y que
y que 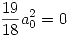 . De la segunda ecuación se ve a simple vista que
. De la segunda ecuación se ve a simple vista que 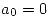 , entonces reemplazando en la primera se obtiene que
, entonces reemplazando en la primera se obtiene que 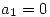 . En conclusión
. En conclusión 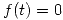
(II)
Se escribe a 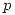 como
como 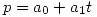
Lo que pide el enunciado es hallar todos los 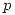 tales que:
tales que:
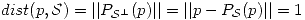
Entonces primero se determina 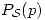 :
:
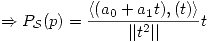
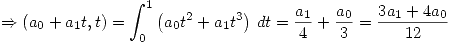
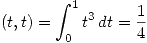
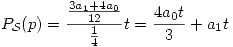
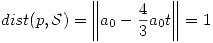
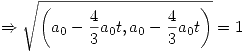
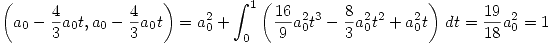
Por lo tanto:
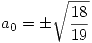 y
y  puede tomar cuaquier valor.
puede tomar cuaquier valor.
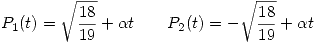
Punto 2
(I)
Considerando 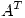 y sabiendo que
y sabiendo que 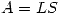 se define
se define 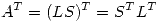 .
. 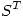 tiene columnas ortonormales y
tiene columnas ortonormales y 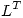 es triangular superior, por lo tanto se plantea una descomposición
es triangular superior, por lo tanto se plantea una descomposición 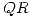 de
de 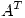 , obteniendo de esta manera
, obteniendo de esta manera 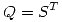 y
y 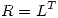 .
.
Se busca una base ortonormal de 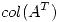 (Gram-Shmidt).
(Gram-Shmidt).

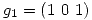
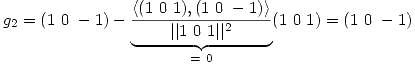
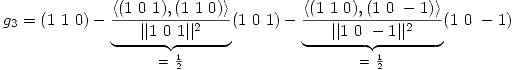
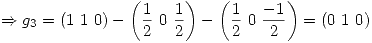
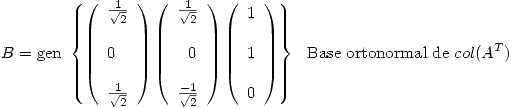
Como 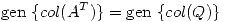
![<tex>Q = \left[ \begin{array}{lll} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ & \\0 & 0 & 1\\ & \\\frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{2}} & 0 \\\end{array} \right] \qquad R = \left[ \begin{array}{lll} \sqrt{2} & 0 & \frac{1}{\sqrt{2}} \\ & \\0 & \sqrt{2} & \frac{1}{\sqrt{2}}\\ & \\0 & 0 & 1 \\\end{array} \right] </tex> <tex>Q = \left[ \begin{array}{lll} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ & \\0 & 0 & 1\\ & \\\frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{2}} & 0 \\\end{array} \right] \qquad R = \left[ \begin{array}{lll} \sqrt{2} & 0 & \frac{1}{\sqrt{2}} \\ & \\0 & \sqrt{2} & \frac{1}{\sqrt{2}}\\ & \\0 & 0 & 1 \\\end{array} \right] </tex>](lib/plugins/latex/images/2dc4e4b3e9aa0a272989c83e0fc058d290134d83_0.png)
![<tex>\Rightarrow A= LS = R^TQ^T = \left[ \begin{array}{lll} 1 & 0 & \ \ 1 \\ & \\1 & 0 & -1\\ & \\1 & 1 & \ \ 0 \\\end{array} \right] </tex> <tex>\Rightarrow A= LS = R^TQ^T = \left[ \begin{array}{lll} 1 & 0 & \ \ 1 \\ & \\1 & 0 & -1\\ & \\1 & 1 & \ \ 0 \\\end{array} \right] </tex>](lib/plugins/latex/images/7a61a2d4646c7683a89d1f85511da5ce9749fdbb_0.png)
(II)

Punto 3
(I)
Para que  se debe cumplir que
se debe cumplir que 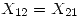
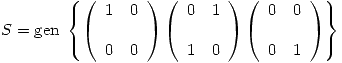
Se toman estos tres elementos para formar una base(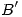 ) de
) de 
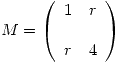
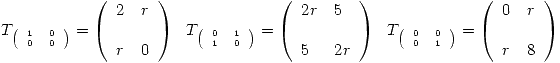
Si 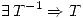 es biyectiva. Por lo tanto lo que hay que determinar son los valores de
es biyectiva. Por lo tanto lo que hay que determinar son los valores de  para los cuales
para los cuales 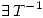 .
.
![<tex>\exists \, T^{-1} \Leftrightarrow \exists \, \left[ T^{-1}\right]_{B^\prime} \Leftrightarrow det\left[T^{-1} \right]_{B^\prime} \neq 0 </tex> <tex>\exists \, T^{-1} \Leftrightarrow \exists \, \left[ T^{-1}\right]_{B^\prime} \Leftrightarrow det\left[T^{-1} \right]_{B^\prime} \neq 0 </tex>](lib/plugins/latex/images/8d7b0f52e1ede560ae5a37071e2bf3bd299dad3c_0.png) .
Que
.
Que ![<tex>det\left[T^{-1}\right]_{B^\prime} \neq 0</tex> <tex>det\left[T^{-1}\right]_{B^\prime} \neq 0</tex>](lib/plugins/latex/images/70026b1eebb34cfece38e3be5619cba665d4af63_0.png) significa que las columnas de
significa que las columnas de ![<tex>\left[T^{-1}\right]_{B^\prime}</tex> <tex>\left[T^{-1}\right]_{B^\prime}</tex>](lib/plugins/latex/images/bae09ed61dfe412affb662c3f59b5c63512e5d1e_0.png) son
son 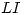 .
.
![<tex> \left[T^{-1}\right]_{B^\prime} = \left[ \begin{array}{lll} 2 & 2r & 0 \\ & \\r & 5 & r\\ & \\0 & 2r & 8\\\end{array} \right] </tex> <tex> \left[T^{-1}\right]_{B^\prime} = \left[ \begin{array}{lll} 2 & 2r & 0 \\ & \\r & 5 & r\\ & \\0 & 2r & 8\\\end{array} \right] </tex>](lib/plugins/latex/images/eac274c00bde3cb2caf9a5e19a805d485af081f6_0.png)
Después de triangular ![<tex>\left[T^{-1}\right]_{B^\prime}</tex> <tex>\left[T^{-1}\right]_{B^\prime}</tex>](lib/plugins/latex/images/bae09ed61dfe412affb662c3f59b5c63512e5d1e_0.png) se obtiene la siguiente matriz:
se obtiene la siguiente matriz:
![<tex> \left[ \begin{array}{lll} 2 & \quad 2r & \quad 0 \\ & \\0 & 2r^2 - 10 & \quad -2r\\ & \\0 & \quad 0 & 20r^2 - 80\\\end{array} \right] </tex> <tex> \left[ \begin{array}{lll} 2 & \quad 2r & \quad 0 \\ & \\0 & 2r^2 - 10 & \quad -2r\\ & \\0 & \quad 0 & 20r^2 - 80\\\end{array} \right] </tex>](lib/plugins/latex/images/39a3a06132b5f136f9c05f0cc1503a9e79586892_0.png)
Para que esta matriz tenga todos sus elementos 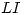 ninguno debe anularse. Por lo tanto de la tercer columna se obtiene que
ninguno debe anularse. Por lo tanto de la tercer columna se obtiene que 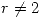 y
y 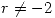 .
.
(II)
![<tex>[T]_{BC} =C_{B^\prime C} [T]_{B^\prime B^\prime} C_{BB^\prime}</tex> <tex>[T]_{BC} =C_{B^\prime C} [T]_{B^\prime B^\prime} C_{BB^\prime}</tex>](lib/plugins/latex/images/2419d3a4e8cb9071648477880a07e4721d6f7277_0.png)
Si ![<tex>[T]_{BC}</tex> <tex>[T]_{BC}</tex>](lib/plugins/latex/images/46b0ce084388c8de425928e8766dad26a05497e6_0.png) y
y ![<tex>[T]_{B^\prime}</tex> <tex>[T]_{B^\prime}</tex>](lib/plugins/latex/images/b85dc6d88324d4e26af0650eabead5b9b8574ead_0.png) son semejantes se cumple que
son semejantes se cumple que ![<tex>rango\left([T]_{BC}\right) = rango \left([T]_{B^\prime}\right)</tex> <tex>rango\left([T]_{BC}\right) = rango \left([T]_{B^\prime}\right)</tex>](lib/plugins/latex/images/ac7bf80d4b75c923e3c3907c8f838fc115ac9739_0.png) .
.
Entonces se debe hallar un valor de  de manera que
de manera que ![<tex>rango \left([T]_{B^\prime}\right) = 2</tex> <tex>rango \left([T]_{B^\prime}\right) = 2</tex>](lib/plugins/latex/images/fe789f1e4cf58019b02bdf2fb42abb015f924304_0.png)
Para que la matriz del inciso anterior sea de rango 2 se debe anular una de las filas. Para  y
y 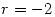 la tercer fila se anula, pero como el enunciado pide los valores de positivos,
la tercer fila se anula, pero como el enunciado pide los valores de positivos,  es el único valor que cumple con la condición planteada.
es el único valor que cumple con la condición planteada.
Entonces:
![<tex> [T]_{B^\prime} = \left[ \begin{array}{lll} 2 & 4 & 0\\ & \\2 & 5 & 2\\ & \\0 & 4 & 8\\\end{array} \right] </tex> <tex> [T]_{B^\prime} = \left[ \begin{array}{lll} 2 & 4 & 0\\ & \\2 & 5 & 2\\ & \\0 & 4 & 8\\\end{array} \right] </tex>](lib/plugins/latex/images/5ee8b18130fc46dc3ea05d8c95cf845af7f0c29c_0.png)
Luego se procede a hallar las bases  y
y  . Se define
. Se define 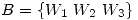 y
y 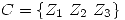 .
.
Con las bases definidas se ve que 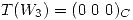 , entonces
, entonces 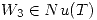 .
Para hallar el núcleo de
.
Para hallar el núcleo de  se plantea:
se plantea:
![<tex>\underbrace{\left[ \begin{array}{lll} 2 & 4 & 0\\ & \\2 & 5 & 2\\ & \\0 & 4 & 8\\\end{array} \right]}_{(*)} \left[ \begin{array}{l} x_1\\\\x_2\\\\x_3\\\end{array} \right] = \left[ \begin{array}{l} 0\\\\0\\\\0\\\end{array} \right] </tex> <tex>\underbrace{\left[ \begin{array}{lll} 2 & 4 & 0\\ & \\2 & 5 & 2\\ & \\0 & 4 & 8\\\end{array} \right]}_{(*)} \left[ \begin{array}{l} x_1\\\\x_2\\\\x_3\\\end{array} \right] = \left[ \begin{array}{l} 0\\\\0\\\\0\\\end{array} \right] </tex>](lib/plugins/latex/images/07c68bdf1586ebddb7a6fdadd979aa58062da948_0.png)
(*) Hay que tener mucho cuidado en este caso ya que esta matriz es ![<tex>[T]_{B^\prime}</tex> <tex>[T]_{B^\prime}</tex>](lib/plugins/latex/images/b85dc6d88324d4e26af0650eabead5b9b8574ead_0.png) y de esta manera estaríamos obteniendo
y de esta manera estaríamos obteniendo  pero en coordenadas de la base
pero en coordenadas de la base 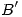 . Se pone énfasis en esto ya que es una de las fuentes de error de este tipo de problemas.
. Se pone énfasis en esto ya que es una de las fuentes de error de este tipo de problemas.
Resolviendo el sistema de ecuaciones se obtiene que:
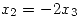 y
y 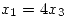 , entonces:
, entonces:
![<tex>Nu(T) = \mbox{gen } \left\{ \left[ \begin{array}{l} -4\\ \\\ \ 2\\\\\ \ 1\\\end{array} \right]_{B^\prime} \right\} \Rightarrow Nu(T) = \mbox{gen } \left\{ \left( \begin{array}{ll} \ \ 4 & -2\\ \\-2 & \ \ 1\\\end{array} \right) \right\}</tex> <tex>Nu(T) = \mbox{gen } \left\{ \left[ \begin{array}{l} -4\\ \\\ \ 2\\\\\ \ 1\\\end{array} \right]_{B^\prime} \right\} \Rightarrow Nu(T) = \mbox{gen } \left\{ \left( \begin{array}{ll} \ \ 4 & -2\\ \\-2 & \ \ 1\\\end{array} \right) \right\}</tex>](lib/plugins/latex/images/c88c27d4f6646f093b741e9bdf3525c86fb337c9_0.png)
Por lo tanto:
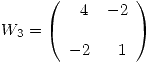
La  esta generada por 2 elementos ya que
esta generada por 2 elementos ya que ![<tex>rango\left([T]_{B^\prime}\right) = 2</tex> <tex>rango\left([T]_{B^\prime}\right) = 2</tex>](lib/plugins/latex/images/8f208617ca8127d398818ebcc72c0a4e44c458c9_0.png) .
.
Se toman dos vectores 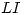 de esta matriz para formar
de esta matriz para formar  teniendo en cuenta que estos vectores estan en coordenadas de la base
teniendo en cuenta que estos vectores estan en coordenadas de la base 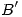 . Entonces:
. Entonces:
![<tex>Im(T) = \mbox{gen } \left\{ \left[ \begin{array}{l} 2\\ \\2\\\\0\\\end{array} \right]_{B^\prime}\left[ \begin{array}{l} 4\\ \\5\\\\4\\\end{array} \right]_{B^\prime} \right\} \Rightarrow Im(T) = \mbox{gen } \left\{ \left( \begin{array}{ll} 2 & 2\\ \\2 & 0\\\end{array} \right) \left( \begin{array}{ll} 4 & 5\\ \\5 & 4\\\end{array} \right) \right\}</tex> <tex>Im(T) = \mbox{gen } \left\{ \left[ \begin{array}{l} 2\\ \\2\\\\0\\\end{array} \right]_{B^\prime}\left[ \begin{array}{l} 4\\ \\5\\\\4\\\end{array} \right]_{B^\prime} \right\} \Rightarrow Im(T) = \mbox{gen } \left\{ \left( \begin{array}{ll} 2 & 2\\ \\2 & 0\\\end{array} \right) \left( \begin{array}{ll} 4 & 5\\ \\5 & 4\\\end{array} \right) \right\}</tex>](lib/plugins/latex/images/bd658cf61aef8dbef99b603a024ef8140ffe9805_0.png)
Luego, sabiendo que  tiene que generar
tiene que generar  se proponen:
se proponen:
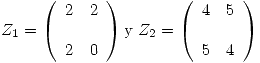
De esta manera 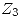 puede ser cualquier elemento
puede ser cualquier elemento 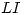 con
con 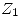 y
y 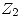 . Además debe pertenecer a
. Además debe pertenecer a  .
.
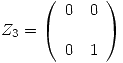
Observando la matriz ![<tex>[T]_{BC}</tex> <tex>[T]_{BC}</tex>](lib/plugins/latex/images/46b0ce084388c8de425928e8766dad26a05497e6_0.png) se aprecia que:
se aprecia que:
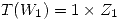
Como 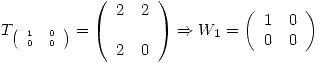
Por otro lado 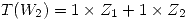 . Utilizando propiedades de transformaciones lineales se puede plantear lo siguiente:
. Utilizando propiedades de transformaciones lineales se puede plantear lo siguiente:
Si se supone 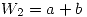 , entonces:
, entonces:
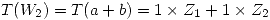
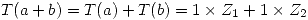
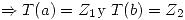
Como 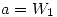 y
y 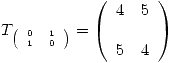 , entonces:
, entonces:
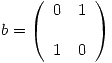
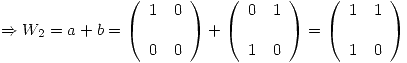
De esta manera quedan definidos todos los elementos de las bases  y
y  .
.
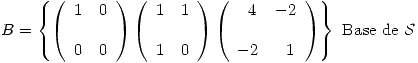
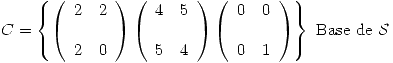
Punto 4
(I)
Si  es solución por cuadrados mínimos de
es solución por cuadrados mínimos de 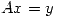 entonces
entonces 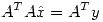
![<tex>A^TA = \left[ \begin{array}{ll} 3 & 0\\\\ 0 & 2\\ \end{array} \right]</tex> <tex>A^TA = \left[ \begin{array}{ll} 3 & 0\\\\ 0 & 2\\ \end{array} \right]</tex>](lib/plugins/latex/images/c1bf431131744215f65330a870866e197e6c3553_0.png)
Se analiza la inversa de 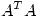 para poder definir
para poder definir 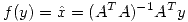
![<tex>(A^TA)^{-1} = \left[ \begin{array}{ll} \frac{1}{3} & 0\\\\ 0 & \frac{1}{2}\\ \end{array} \right]</tex> <tex>(A^TA)^{-1} = \left[ \begin{array}{ll} \frac{1}{3} & 0\\\\ 0 & \frac{1}{2}\\ \end{array} \right]</tex>](lib/plugins/latex/images/d0fa69063d0529c419fccc107f4b7476bd102918_0.png)
Por definición 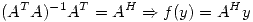
Para que  sea lineal se debe cumplir:
sea lineal se debe cumplir:
- (a)
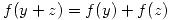
- (b)
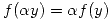
(a) 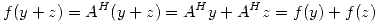
(b) 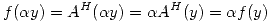
Se procede a hallar la representación matricial de  en las bases canónicas:
en las bases canónicas:

![<tex>f(1\ 0\ 0) = A^H\left[ \begin{array}{l} 1\\ \\0\\\\ 0\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3} & 0\\\\ 0 & \frac{1}{2}\\ \end{array} \right] \left[ \begin{array}{l} 1\\\\ 1\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3}\\\\ \frac{1}{2}\\\end{array} \right]</tex> <tex>f(1\ 0\ 0) = A^H\left[ \begin{array}{l} 1\\ \\0\\\\ 0\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3} & 0\\\\ 0 & \frac{1}{2}\\ \end{array} \right] \left[ \begin{array}{l} 1\\\\ 1\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3}\\\\ \frac{1}{2}\\\end{array} \right]</tex>](lib/plugins/latex/images/70dfc7d8687a311783cc4359b77ff8013576b587_0.png)
![<tex>f(0\ 1\ 0) = A^H\left[ \begin{array}{l} 0\\ \\1\\\\ 0\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3} & 0\\\\ 0 & \frac{1}{2}\\ \end{array} \right] \left[ \begin{array}{l} 1\\\\ 0\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3}\\\\ 0\\\end{array} \right]</tex> <tex>f(0\ 1\ 0) = A^H\left[ \begin{array}{l} 0\\ \\1\\\\ 0\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3} & 0\\\\ 0 & \frac{1}{2}\\ \end{array} \right] \left[ \begin{array}{l} 1\\\\ 0\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3}\\\\ 0\\\end{array} \right]</tex>](lib/plugins/latex/images/5aeb7bb5e4bfabf1c8f1aa7f2c4cb313bccdd1b1_0.png)
![<tex>f(0\ 0\ 1) = A^H\left[ \begin{array}{l} 0\\ \\0\\\\ 1\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3} & 0\\\\ 0 & \frac{1}{2}\\ \end{array} \right] \left[ \begin{array}{l} -1\\\\ \ \ 1\\ \end{array} \right] = \left[ \begin{array}{ll} -\frac{1}{3}\\\\ \ \ \frac{1}{2}\\\end{array} \right]</tex> <tex>f(0\ 0\ 1) = A^H\left[ \begin{array}{l} 0\\ \\0\\\\ 1\\ \end{array} \right] = \left[ \begin{array}{ll} \frac{1}{3} & 0\\\\ 0 & \frac{1}{2}\\ \end{array} \right] \left[ \begin{array}{l} -1\\\\ \ \ 1\\ \end{array} \right] = \left[ \begin{array}{ll} -\frac{1}{3}\\\\ \ \ \frac{1}{2}\\\end{array} \right]</tex>](lib/plugins/latex/images/483972632879c4e781cddf68a506b4747dff2cfd_0.png)
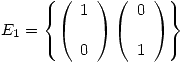
![<tex> [T]_{E_1E_2} = \left[ \begin{array}{lll} \frac{1}{3} & \frac{1}{3} & -\frac{1}{3}\\\\ \frac{1}{2} & 0 & \ \ \frac{1}{2}\\\end{array} \right]</tex> <tex> [T]_{E_1E_2} = \left[ \begin{array}{lll} \frac{1}{3} & \frac{1}{3} & -\frac{1}{3}\\\\ \frac{1}{2} & 0 & \ \ \frac{1}{2}\\\end{array} \right]</tex>](lib/plugins/latex/images/fea05909217cb3296a5984b64f4a97fd84ff98dd_0.png)
(II)
Para hallar la imagen y núcleo de  se trabaja con
se trabaja con ![<tex>[T]_{E_1E_2}</tex> <tex>[T]_{E_1E_2}</tex>](lib/plugins/latex/images/c8b6f6d9cc7333262f2d79c8267c7b3add57c85f_0.png) .
.
Para hallar el núcleo se plantea lo siguiente:
![<tex> \left[ \begin{array}{lll} \frac{1}{3} & \frac{1}{3} & -\frac{1}{3}\\\\ \frac{1}{2} & 0 & \ \ \frac{1}{2}\\\end{array} \right]\underbrace{\left[ \begin{array}{l} x_1\\\\ x_2\\\\x_3\\\end{array} \right]}_{(*)} = \left[ \begin{array}{l} 0\\\\ 0\\\\0\\\end{array} \right]</tex> <tex> \left[ \begin{array}{lll} \frac{1}{3} & \frac{1}{3} & -\frac{1}{3}\\\\ \frac{1}{2} & 0 & \ \ \frac{1}{2}\\\end{array} \right]\underbrace{\left[ \begin{array}{l} x_1\\\\ x_2\\\\x_3\\\end{array} \right]}_{(*)} = \left[ \begin{array}{l} 0\\\\ 0\\\\0\\\end{array} \right]</tex>](lib/plugins/latex/images/28fc3e9fa47b58d2807420b3eeff889348bfe311_0.png)
(*) Este vector esta en coordenadas de la base canónica de 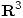 .
.
de este sistema de ecuaciones se obtiene lo siguiente:
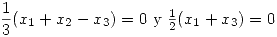 , entonces:
, entonces:
![<tex>Nu(T) = \mbox{gen } \left\{ \left[ \begin{array}{l} \ \ 1\\ \\-2\\\\-1\\\end{array} \right]_{E_1} \right\} \underbrace{=}_{(**)} \mbox{gen } \left\{ \left( \begin{array}{ll} \ \ 1\\ \\-2\\\\-1\\\end{array} \right) \right\}</tex> <tex>Nu(T) = \mbox{gen } \left\{ \left[ \begin{array}{l} \ \ 1\\ \\-2\\\\-1\\\end{array} \right]_{E_1} \right\} \underbrace{=}_{(**)} \mbox{gen } \left\{ \left( \begin{array}{ll} \ \ 1\\ \\-2\\\\-1\\\end{array} \right) \right\}</tex>](lib/plugins/latex/images/d8cef209bb078b7a3a17cbfac4326abce89d42e7_0.png)
(**) Esta igualdad se da ya que 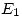 y
y  son bases canónicas y por isomorfismo de coordenadas los vectores y sus coordenadas coinciden.
son bases canónicas y por isomorfismo de coordenadas los vectores y sus coordenadas coinciden.
Entonces:
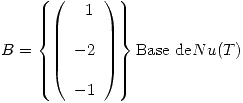
Luego:
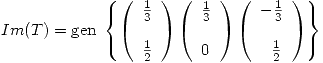
Para hallar una base de  solo de debe quitar uno de estos tres vectores que sea $LD$.
Entonces:
solo de debe quitar uno de estos tres vectores que sea $LD$.
Entonces:
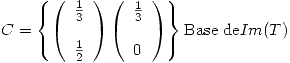
Discusión
El enunciado del primer punto dice que el PI es f(0) + g(0) + la integral. De esa manera no es PI. Luego, en la resolución primero toma que es f(0) + g(0) + la integral pero luego lo toma como si fuese f(0)*g(0) + la integral. De esa forma si es PI. Espero haberme explicado bien.
FIXED