Examen Parcial - 61.08. Álgebra II
Cátedra: Curso 01
Fecha: 1º Oportunidad - (1º Cuatrimestre|Invierno) 2007
Día: 10/05/2003
Punto I
Sea  con
con 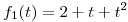 ,
, 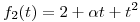 y
y  . Se pide:
. Se pide:
(a) Determinar todos los valores de  para los que está bien definida
para los que está bien definida 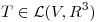 tal que
tal que ![<tex>T(f_1)=[1, 1, 1]^T</tex> <tex>T(f_1)=[1, 1, 1]^T</tex>](lib/plugins/latex/images/e38b490da784f9bec2e5be9c24ad5f55fc4c4bc8_0.png) ,
, ![<tex>T(f_2)=[1,,-1,1]</tex> <tex>T(f_2)=[1,,-1,1]</tex>](lib/plugins/latex/images/5f1d2c09fb4cbdcd9f14879efde2270dfd26c3cf_0.png) y
y ![<tex>T(f_3)=[2,0,2]^T</tex> <tex>T(f_3)=[2,0,2]^T</tex>](lib/plugins/latex/images/bbc1401944a53c05993a2246d2835f22d3d42c79_0.png) . Para esos valores de
. Para esos valores de  hallar bases de
hallar bases de  e
e 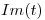 .
.
(b) para la transformación lineal  del punto a, con
del punto a, con 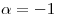 , decidir para qué valores de
, decidir para qué valores de  existirán bases
existirán bases  de
de  y
y 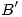 de
de 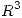 tales que
tales que ![<tex>[T]_{BB'}= \left[ \begin{array}{ccc} 0 & 3 & 1\\ 0 & 2 & 1\\ \lambda -1 & \lambda +2 & 1 \end{array} \right]</tex> <tex>[T]_{BB'}= \left[ \begin{array}{ccc} 0 & 3 & 1\\ 0 & 2 & 1\\ \lambda -1 & \lambda +2 & 1 \end{array} \right]</tex>](lib/plugins/latex/images/435b2b888f98062ff939bea583841a6438d28054_0.png) . Encontrar
. Encontrar  y
y 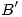 .
.
Punto II
(a) Encontrar 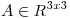 tal que
tal que ![<tex>[0,-1,1]A=0</tex> <tex>[0,-1,1]A=0</tex>](lib/plugins/latex/images/54d1f3679209c0a5b02582592db6229472f6f609_0.png) y
y  admita una descomposición
admita una descomposición 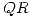 normalizada
normalizada 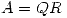 con
con ![<tex>R= \left[ \begin{array}{ccc} 2 \sqrt{2} & \sqrt{2} & 2 \sqrt{2}\\ 0 & \sqrt{3} & 2 \sqrt{3}\\ \end{array} \right]</tex> <tex>R= \left[ \begin{array}{ccc} 2 \sqrt{2} & \sqrt{2} & 2 \sqrt{2}\\ 0 & \sqrt{3} & 2 \sqrt{3}\\ \end{array} \right]</tex>](lib/plugins/latex/images/0e29d1a04f7c43ea5fc8070bff1e291ed95a9334_0.png) . Es única?
. Es única?
(b) Hallar, para la matriz  de a, la matriz de proyección sobre
de a, la matriz de proyección sobre ![<tex>[Col(A)]^{\perp}</tex> <tex>[Col(A)]^{\perp}</tex>](lib/plugins/latex/images/375e6910e1d7c72307bdb5b66754cb37cfb85213_0.png) .
.
Punto III
(a) Demostrar que 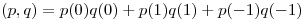 es producto interno en
es producto interno en 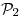 pero no en
pero no en 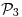
(b) Hallar los valores de  y
y 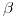 para que
para que 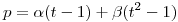 se encuentre lo más cerca posible de
se encuentre lo más cerca posible de 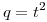 , considerando el producto interno definido en a.
, considerando el producto interno definido en a.
Hallar 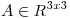 tal que
tal que ![<tex>P= \left[ \begin{array}{cc} 1/2 & 1/2\\ 1/2 & 1/2 \\ \end{array} \right]</tex> <tex>P= \left[ \begin{array}{cc} 1/2 & 1/2\\ 1/2 & 1/2 \\ \end{array} \right]</tex>](lib/plugins/latex/images/6ed4e41c74cec092ece66aab187b6d557ae07193_0.png) proyecte sobre
proyecte sobre 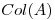 ;
; 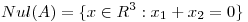 y
y 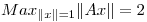 .
.
Punto IV
Sea 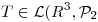 tal que
tal que ![<tex>[T]_{EB}= \left[ \begin{array}{ccc} 1 & 4 & 0\\ -2 & 1 & 3\\ \lambda ^2 & 4 \lambda +3 & 1 \end{array} \right]</tex> <tex>[T]_{EB}= \left[ \begin{array}{ccc} 1 & 4 & 0\\ -2 & 1 & 3\\ \lambda ^2 & 4 \lambda +3 & 1 \end{array} \right]</tex>](lib/plugins/latex/images/5d0dd0b2577c5cc4223874e3bdf9b46a7da68512_0.png) con
con 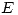 la base canónica de
la base canónica de 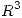 y
y 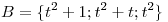 . Se pide:
. Se pide:
(a)
i) Hallar los valores de  para que
para que  sea inversible.
ii)Para
sea inversible.
ii)Para 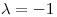 justificar que
justificar que  es biyectiva, explicar cómo se obtiene
es biyectiva, explicar cómo se obtiene ![<tex>[T^{-1}]_{EE'}</tex> <tex>[T^{-1}]_{EE'}</tex>](lib/plugins/latex/images/663e5513351f09488fb44d22c1811bcb5ab6aef2_0.png) a partir de
a partir de ![<tex>[T]_{EB}</tex> <tex>[T]_{EB}</tex>](lib/plugins/latex/images/b21e191926ffa9cc2b80fb346e68f225f3f295b1_0.png) (Con
(Con 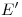 la base canónica de
la base canónica de 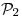 y calcular
y calcular 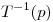 para
para 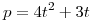 .
.
(b) Hallar los valores de  para que existan al menos dos
para que existan al menos dos 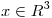 distintos, tales que
distintos, tales que  .
.
El examen se aprueba resolviendo correctamente cuatro puntos, entre los cuales debe figurar uno del ejercicio 1 ó 4 y uno del 2 ó 3. Justificar todas las respuestas.
