Examen Final - 61.08. Álgebra II A - 07/08/2008
Cátedra: Indistinta
Fecha: 4º Oportunidad - Invierno 2008
Día: 07/08/2008
Enunciado
Punto 1
Resolver el problema 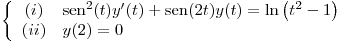 , especificando dominio de existencia y unicidad de la solución.
, especificando dominio de existencia y unicidad de la solución.
Punto 2
Sea 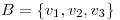 una base de un
una base de un  -espacio vectorial
-espacio vectorial  y sea
y sea  tal que
tal que  ,
, 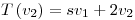 y
y 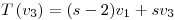 . Hallar todos los
. Hallar todos los 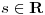 para los cuales existe una base de
para los cuales existe una base de  compuesta por autovectores de
compuesta por autovectores de  y exhibir una de esas bases (en términos de la base
y exhibir una de esas bases (en términos de la base  ).
).
Punto 3
Sea 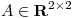 la matriz de proyección sobre
la matriz de proyección sobre 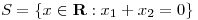 y sea
y sea 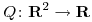 la forma cuadrática dada por
la forma cuadrática dada por  . Determinar, si existen,
. Determinar, si existen, 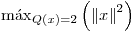 y
y 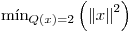 y los puntos donde se alcanzan estos valores.
y los puntos donde se alcanzan estos valores.
Punto 4
Encontrar la solución del sistema 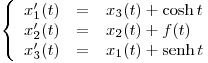 donde la función
donde la función 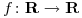 verifica
verifica 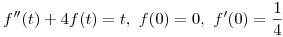 .
.
Punto 5
Dada ![<tex>A = \left[ \begin{array}{ccc} 1 & -2 & \phantom{-}0\\ 1 & \phantom{-}1 & -1\\ 1 & \phantom{-}1 & \phantom{-}1\end{array} \right] \left[ \begin{array}{cc} 2 & 0\\ 0 & 2\\ 0 & 0\end{array} \right] \left[ \begin{array}{cc} \frac{1}{\sqrt{2}} & \phantom{-}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array} \right]</tex> <tex>A = \left[ \begin{array}{ccc} 1 & -2 & \phantom{-}0\\ 1 & \phantom{-}1 & -1\\ 1 & \phantom{-}1 & \phantom{-}1\end{array} \right] \left[ \begin{array}{cc} 2 & 0\\ 0 & 2\\ 0 & 0\end{array} \right] \left[ \begin{array}{cc} \frac{1}{\sqrt{2}} & \phantom{-}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array} \right]</tex>](lib/plugins/latex/images/706b1b29be719485c3b40486884cae6009fc01e3_0.png) , hallar la matriz de proyección sobre el espacio ortogonal a
, hallar la matriz de proyección sobre el espacio ortogonal a  y calcular
y calcular  .
.
Justifique todas sus respuestas. Numere las hojas y firme al final del examen.
El examen se aprueba resolviendo correctamente 3 (tres) ejercicios.
Resolución
Punto 1
Yo lo resolvi de esta manera..
El tema pasa por recordar una de las viejas propiedades de trigonometria:
sen(t+u) = sen(t)cos(u) + sen(u)cos(t)
Entonces sen(2t) = sen(t)cos(t) + sen(t)cos(t) = 2sen(t)cos(t)
Luego la derivada de sen²(t) si la calculamos con una sustitución de sen(t)=v y dv = d(sen(t)) = cos(t) quedaria:
d(v²) = 2v dv = 2sen(t) d(sen(t)) = 2sen(t)cos(t) = sen(2t)
Por lo tanto la ec diferencial se reduce a:
sen²(t)y'(t) + sen(2t)y(t) = [sen²(t)y(t)]' = ln(t²-1)
Integrando en ambos miembros queda… sen²(t)y(t) = ∫ln(t²-1)dt
Por lo tanto.. y(t) = [∫ln(t²-1)]/sen²(t) = {2[ln(t²-1)-2] + ln(t+1) - ln(t-1) + c} / sen²(t)
Luego c = -3ln(3)+4 –> c = -ln(27)+4
Quedaria y(t) = {2[ln(t²-1)-2] + ln(t+1) - ln(t-1) - ln(27) + 4} / sen²(t)
Finalmente agrupando logaritmos
y(t) = ln[(t²-1)²(t+1)/27(t-1)] / sen²(t)
sabiendo que (t²-1)=(t+1)(t-1)…
y(t) = ln[(t+1)³(t-1)/27] / sen²(t)
Comment: Ya se.. es una expresion horriblee en ambas formas.. pero la probe diferenciandola y encaja perfectamente como solución
Discusión
Bueno, si ven algo incorrecto lo discutimos para corregirlo
«El Tano»
