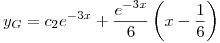Examen Final - 61.08. Álgebra II A - 07/03/2008
Cátedra: Indistinta
Fecha: 5º Oportunidad - 2º Cuatrimestre 2008
Día: 07/03/2008
Enunciado
Punto 1
a)
Sea 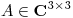 y sea
y sea 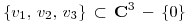 tal que
tal que 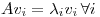 y
y 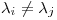 si
si 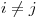 . Probar que si
. Probar que si  , entonces
, entonces 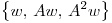 es base de
es base de 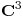 .
.
b)
Sea 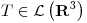 tal que
tal que ![<tex>[T]_{EB} = \left( \begin{array}{ccc} \alpha +1 & 1 & 0 \\ - \alpha - 1 & 0 & 0 \\ \alpha +1 & 0 & -1 \end{array} \right)</tex> <tex>[T]_{EB} = \left( \begin{array}{ccc} \alpha +1 & 1 & 0 \\ - \alpha - 1 & 0 & 0 \\ \alpha +1 & 0 & -1 \end{array} \right)</tex>](lib/plugins/latex/images/971728b26a04d6884dc0f95ef5f5e65d3dc1444c_0.png) con
con 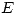 la base canónica y
la base canónica y 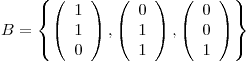 . Hallar todos los valores de
. Hallar todos los valores de  para los cuales existe una base
para los cuales existe una base 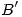 tal que
tal que ![<tex>[T]_{B'}</tex> <tex>[T]_{B'}</tex>](lib/plugins/latex/images/4098bfd733886eb8cc791eb0864b2ae36e654953_0.png) es diagonal.
es diagonal.
Punto 2
a)
Probar que si 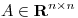 es simétrica y
es simétrica y  , entonces
, entonces
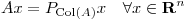 .
.
b)
Definir un producto interno  en
en 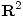 tal que
tal que 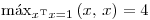 ,
, 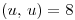 para
para 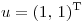 y
y 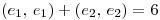 si
si 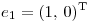 y
y 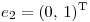
Punto 3
a)
Sea 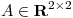 simétrica tal que
simétrica tal que 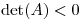 . Determinar, justificando la respuesta, qué clase de curva define
. Determinar, justificando la respuesta, qué clase de curva define 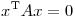 .
.
b)
Hallar la representación matricial en la base canónica de la transformación lineal 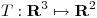 , definida como: dado
, definida como: dado 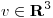 , entonces
, entonces 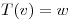 si
si 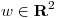 es el vector de menor norma que satisface
es el vector de menor norma que satisface 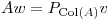 .
.
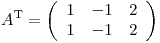
Punto 4
a)
Hallar la solución general del siguiente sistema: 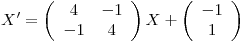 .
.
b)
Hallar todas las soluciones de:  que tienen límite finito cuando
que tienen límite finito cuando  .
.
Resolución A
Punto 2
a)
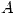 es simetrica, por lo tanto
es simetrica, por lo tanto 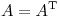
Como 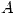 es simetrica, entonces se puede diagonalizar ortogonalmente.
es simetrica, entonces se puede diagonalizar ortogonalmente.
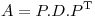
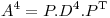
Y el enunciado nos da el dato de :

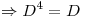
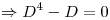
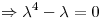
Los unicos avas que cumplen eso son : 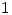 y
y 
Si 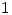 y
y  son sus autovalores, entonces:
son sus autovalores, entonces:
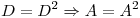
Y como demostre que :
 y que
y que 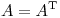 entonces A es matriz de proyeccion.
entonces A es matriz de proyeccion.
b)
Para una forma cuadratica de la forma 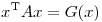 con
con 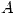 simetrica y definida positiva, la forma cuadratica define un producto interno. Entonces puedo definir una matriz
simetrica y definida positiva, la forma cuadratica define un producto interno. Entonces puedo definir una matriz
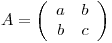 .
.
Del dato de que 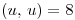 con
con 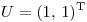 resuelvo
resuelvo
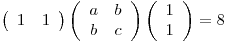
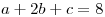
Hago lo mismo con los canónicos
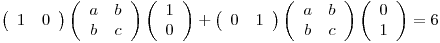
Y obtengo que 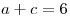
Despejando de la otra ecuacion queda que 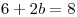

Del dato que 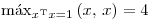 , como estoy en norma 1, se que 4 sera el autovalor máximo, por lo tanto raíz máxima del polinomio caracteristico de
, como estoy en norma 1, se que 4 sera el autovalor máximo, por lo tanto raíz máxima del polinomio caracteristico de 
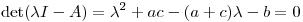
como  satisface la ecuacion por ser autovector, y tenemos que
satisface la ecuacion por ser autovector, y tenemos que 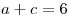
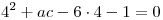

ahi despeje a y c y obtuve 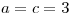
por lo tanto la matriz que genera el producto interno es
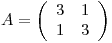
Solo falta multiplicar la matriz por los vectores genericos para obtener 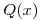
Punto 3
a)
Sabemos que:
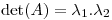
Como 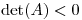 entonces los signo de
entonces los signo de 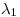 y
y 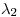 son diferentes.
son diferentes.
Hago el cambio de variables para eliminar los productos cruzados:
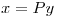 y me queda:
y me queda:
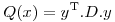
Igualo a cero:
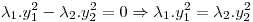
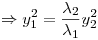
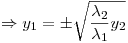
Con lo cual nos quedan dos rectas:
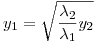 y
y 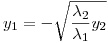
Resolución B
Punto 1
a)
H)
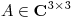
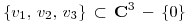
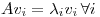 y
y 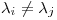 si
si 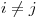

T)
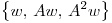 es base de
es base de 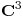
Es decir, 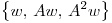 son LI y generan
son LI y generan 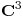
D)
Ni  ni
ni  ni
ni 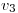 son nulos, y
son nulos, y
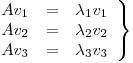 Luego,
Luego,  ,
,  y
y 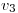 son autovectores de
son autovectores de 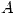 .
.
Por otro lado, como 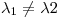 ,
, 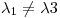 ,
, 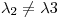 , el conjunto
, el conjunto 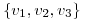 es LI.
es LI.
¿Cómo se si 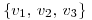 es base?
es base?
O sea, ¿cómo se si 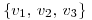 genera
genera 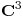
Pues bien, 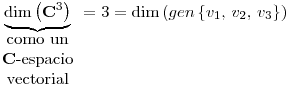 y como
y como 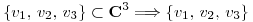 genera
genera 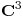 y por tanto es base.
y por tanto es base.
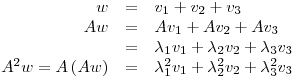
Entonces:
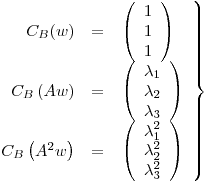 Si
Si 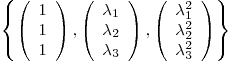 es LI
es LI 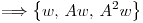 es LI.
es LI.
sub-T)
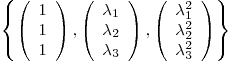 LI.
LI.
AT) (antítesis)
Supongamos que es LD. Entonces:
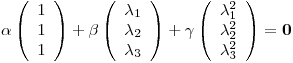 con
con 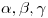 no todos cero.
no todos cero.
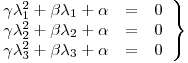 En general, cada uno de estos tres polinomios tiene dos soluciones distintas,
En general, cada uno de estos tres polinomios tiene dos soluciones distintas, 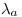 y
y 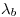 , tal que:
, tal que:
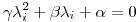 con
con 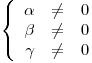
Pero entonces cada 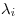 puede tomar sólo dos valores, y como
puede tomar sólo dos valores, y como 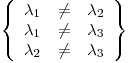 hemos llegado a un absurdo.
hemos llegado a un absurdo.
El conjunto 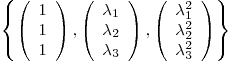 es LI y entonces también lo es
es LI y entonces también lo es 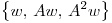 .
.
Pero, ¿genera 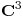 ?
?
Veamos: 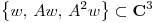 pues
pues 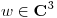 y
y 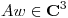 y
y 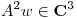 y
y 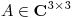
Además, 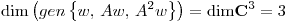
y entonces 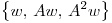 es base de
es base de 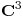 QUOD ERAT DEMONSTRANDUM.
QUOD ERAT DEMONSTRANDUM.
b)
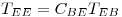
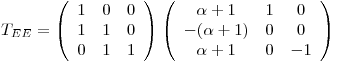
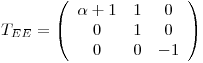
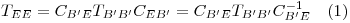
Entonces 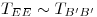
y por tanto los avales de 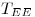 son los de
son los de 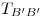 con igual mg y ma.
con igual mg y ma.
Más aún, como 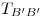 debe ser diagonal,
debe ser diagonal, 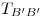 contiene a los avales de
contiene a los avales de 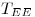 en su diagonal. Dichos avales son:
en su diagonal. Dichos avales son:
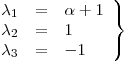 pues
pues 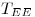 es triangular.
es triangular.
Para que 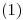 se cumpla,
se cumpla, 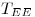 debe ser diagonalizable. Para ello, o bien:
debe ser diagonalizable. Para ello, o bien:
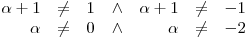
o bien:
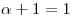 y
y 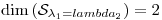
o bien:
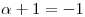 y
y 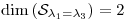
(Faltan ver las condiciones sobre  en los dos últimos casos).
en los dos últimos casos).
Punto 2
a)
H)
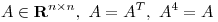
T)
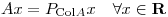
D)
Como 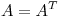
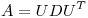 con
con 
 y si
y si 
Entonces:
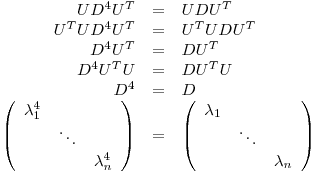
Si 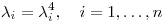 :
:
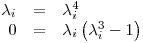
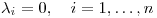 o bien
o bien 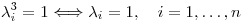
En resumen: cada 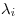 puede ser ó 0 ó 1.
puede ser ó 0 ó 1.
![<tex>\begin{array}[b]{rcl} A^T & = & A\\ A & = & UDU^T\\ A^T & = & UD^TU^T = UDU^T \end{array} \mbox{ pues } D \mbox{ es diagonal.}</tex> <tex>\begin{array}[b]{rcl} A^T & = & A\\ A & = & UDU^T\\ A^T & = & UD^TU^T = UDU^T \end{array} \mbox{ pues } D \mbox{ es diagonal.}</tex>](lib/plugins/latex/images/b5b659b0be0e824b0b2b51b6ea5fe8e553421159_0.png)
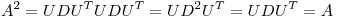 pues
pues 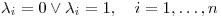 , entonces
, entonces 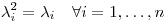 y entonces
y entonces 
Como 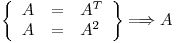 es matriz de proyección, y proyecta sobre
es matriz de proyección, y proyecta sobre 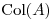
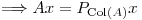 c.q.d.
c.q.d.
b)
Para definir un PI en 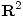 puedo usar una matriz
puedo usar una matriz 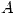 simétrica y definida positiva,
simétrica y definida positiva, 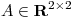
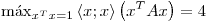
¿Cómo garantizo esto?
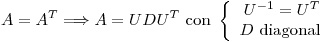
![<tex>\begin{array}{rcl} x^TAx & = & x^TUDU^Tx\\x^TAx & = & y^TDy \mbox{ con } y=U^Tx \Rightarrow y^T=x^TU\\ & = & \left[\begin{array}{cc} y_1 & y_2 \end{array}\right] \left( \begin{array}{cc} \lambda_1\\ & \lambda_2 \end{array} \right) \left[ \begin{array}{c} y_1\\ y_2 \end{array} \right]\\ & = & \lambda_1 y_1^2+\lambda_2 y_2^2 \mbox{ con } \lambda_i \mbox{ aval de } A\end{array}</tex> <tex>\begin{array}{rcl} x^TAx & = & x^TUDU^Tx\\x^TAx & = & y^TDy \mbox{ con } y=U^Tx \Rightarrow y^T=x^TU\\ & = & \left[\begin{array}{cc} y_1 & y_2 \end{array}\right] \left( \begin{array}{cc} \lambda_1\\ & \lambda_2 \end{array} \right) \left[ \begin{array}{c} y_1\\ y_2 \end{array} \right]\\ & = & \lambda_1 y_1^2+\lambda_2 y_2^2 \mbox{ con } \lambda_i \mbox{ aval de } A\end{array}</tex>](lib/plugins/latex/images/59eaab24ba24040a3005c73c9f141c66a7107cf9_0.png)
Si 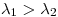 , entonces:
, entonces:

![<tex>\mbox{Aclaraci\'on: } \begin{array}[t]{rcl} y^Ty & = & {\left( U^Tx \right)}^T U^Tx\\y^Ty & = & x^T UU^T x\\y^Ty & = & x^Tx = 1\end{array}</tex> <tex>\mbox{Aclaraci\'on: } \begin{array}[t]{rcl} y^Ty & = & {\left( U^Tx \right)}^T U^Tx\\y^Ty & = & x^T UU^T x\\y^Ty & = & x^Tx = 1\end{array}</tex>](lib/plugins/latex/images/7fada195d61a29bd0d6c4b546567b30a1c87bcfc_0.png)
Con 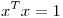 , el máximo impuesto es igual al valor del máximo aval de
, el máximo impuesto es igual al valor del máximo aval de 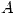 . Dicho aval,
. Dicho aval, 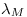 , debe ser 4.
, debe ser 4.
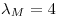
Por otro lado, como 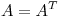 y es def. positiva, sus avales
y es def. positiva, sus avales 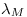 y
y 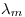 deben ser mayores a cero.
deben ser mayores a cero.
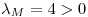 OK
OK
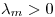
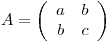 , entonces
, entonces 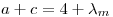 .
.
![<tex>\begin{array}{rcl} \left\langle u ; u \right\rangle = 8 = \left[ \begin{array}{cc} 1 & 1 \end{array} \right] \left( \begin{array}{cc} a & b\\ b & c \end{array} \right) \left[ \begin{array}{c} 1\\ 1 \end{array} \right] &=& \left[ \begin{array}{cc} a+b & b+c \end{array} \right] \left[ \begin{array}{c} 1\\ 1 \end{array} \right]\\ & = & a+b+b+c = 8\\ & = & a+c + 2b =8 \end{array}</tex> <tex>\begin{array}{rcl} \left\langle u ; u \right\rangle = 8 = \left[ \begin{array}{cc} 1 & 1 \end{array} \right] \left( \begin{array}{cc} a & b\\ b & c \end{array} \right) \left[ \begin{array}{c} 1\\ 1 \end{array} \right] &=& \left[ \begin{array}{cc} a+b & b+c \end{array} \right] \left[ \begin{array}{c} 1\\ 1 \end{array} \right]\\ & = & a+b+b+c = 8\\ & = & a+c + 2b =8 \end{array}</tex>](lib/plugins/latex/images/c5adb3f4c60989a30fb8a96fa04791d1b7c5729f_0.png)
![<tex>\begin{array}{rcl} \left\langle e_1 ; e_1 \right\rangle + \left\langle e_2;e_2 \right\rangle &=& 6\\e_1^TAe_1+e_2^TAe_2 &=& 6\\\left[ \begin{array}{cc} 1 & 0 \end{array} \right] \left( \begin{array}{cc} a & b\\ b & c \end{array} \right) \left[ \begin{array}{c} 1\\ 0 \end{array} \right] + \left[ \begin{array}{cc} 0 & 1 \end{array} \right] \left( \begin{array}{cc} a & b\\ b & c \end{array} \right) \left[ \begin{array}{c} 0\\ 1 \end{array} \right]&=& 6\\\left[ \begin{array}{cc} a & b \end{array} \right] \left[ \begin{array}{c} 1\\ 0 \end{array} \right] + \left[ \begin{array}{cc} b & c \end{array} \right] \left[ \begin{array}{c} 0\\ 1 \end{array} \right]&=& 6\\a+c &=& 6\\4+\lambda_m &=& 6\\\lambda_m &=& 2 \end{array}</tex> <tex>\begin{array}{rcl} \left\langle e_1 ; e_1 \right\rangle + \left\langle e_2;e_2 \right\rangle &=& 6\\e_1^TAe_1+e_2^TAe_2 &=& 6\\\left[ \begin{array}{cc} 1 & 0 \end{array} \right] \left( \begin{array}{cc} a & b\\ b & c \end{array} \right) \left[ \begin{array}{c} 1\\ 0 \end{array} \right] + \left[ \begin{array}{cc} 0 & 1 \end{array} \right] \left( \begin{array}{cc} a & b\\ b & c \end{array} \right) \left[ \begin{array}{c} 0\\ 1 \end{array} \right]&=& 6\\\left[ \begin{array}{cc} a & b \end{array} \right] \left[ \begin{array}{c} 1\\ 0 \end{array} \right] + \left[ \begin{array}{cc} b & c \end{array} \right] \left[ \begin{array}{c} 0\\ 1 \end{array} \right]&=& 6\\a+c &=& 6\\4+\lambda_m &=& 6\\\lambda_m &=& 2 \end{array}</tex>](lib/plugins/latex/images/c81554fbcb450ad9f454312621aeb1f05d76c3f9_0.png)
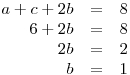
Ahora supongamos que  y que
y que  , se cumple que
, se cumple que 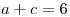 , y
, y 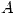 queda:
queda: 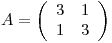 .
.
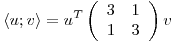
Punto 3
a)
![<tex>\begin{array}[b]{rcl}A&=&A^T\\\Rightarrow A&=& UDU^T\end{array} \mbox{ con } U^T=U^{-1} \mbox{ y } D=\left(\begin{array}{cc} \lambda_1 \\ & \lambda_2 \end{array}\right)</tex> <tex>\begin{array}[b]{rcl}A&=&A^T\\\Rightarrow A&=& UDU^T\end{array} \mbox{ con } U^T=U^{-1} \mbox{ y } D=\left(\begin{array}{cc} \lambda_1 \\ & \lambda_2 \end{array}\right)</tex>](lib/plugins/latex/images/0b61ee565ad88b6e797db2e7b0ab85edd053d271_0.png) con
con 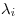 aval de
aval de 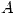
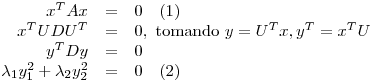
Además, es 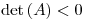 , y como
, y como  ,
, 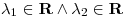 , y como
, y como 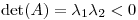 , uno de los avales es positivo y el otro es negativo, con lo cual la ecuación
, uno de los avales es positivo y el otro es negativo, con lo cual la ecuación 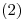 resulta (con
resulta (con 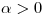 y
y  ):
):
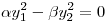 ó
ó 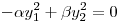
Vemos también que 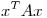 está igualado a cero.
está igualado a cero.
La curva es, pues, una hipérbola degenerada en dos rectas.
b)
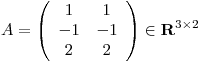
![<tex>A=U_r D_{r\times r} V_r^T \mbox{ con } \begin{array}[t]{r@{=}ccl} U_r & \left[ \parbox{30pt}{\centering BON de Col($A$)} \right] &\in& \mathbf{R}^{3\times1}\\D_{r\times r} & \sigma &\in& \mathbf{R}^{1\times1}\\V_r & \left[ \parbox{30pt}{\centering BON de Fil($A$)} \right] &\in& \mathbf{R}^{2\times1}\end{array}</tex> <tex>A=U_r D_{r\times r} V_r^T \mbox{ con } \begin{array}[t]{r@{=}ccl} U_r & \left[ \parbox{30pt}{\centering BON de Col($A$)} \right] &\in& \mathbf{R}^{3\times1}\\D_{r\times r} & \sigma &\in& \mathbf{R}^{1\times1}\\V_r & \left[ \parbox{30pt}{\centering BON de Fil($A$)} \right] &\in& \mathbf{R}^{2\times1}\end{array}</tex>](lib/plugins/latex/images/2a420cbb79e0465092aba956207916b228e1b868_0.png)
![<tex>A=\frac{\left[ \begin{array}{c} 1 \\ -1 \\ 2 \end{array} \right]}{\sqrt{6}} \sigma \frac{\left[ \begin{array}{cc} 1 & 1 \end{array} \right]}{\sqrt{2}}</tex> <tex>A=\frac{\left[ \begin{array}{c} 1 \\ -1 \\ 2 \end{array} \right]}{\sqrt{6}} \sigma \frac{\left[ \begin{array}{cc} 1 & 1 \end{array} \right]}{\sqrt{2}}</tex>](lib/plugins/latex/images/6a9b868fba4e7917132972522d6d44aabacdde4f_0.png) donde
donde 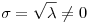 , donde
, donde  es un aval distinto de cero de
es un aval distinto de cero de 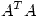 .
.
![<tex>A^TA= \left[ \begin{array}{ccc} 1 & -1 & 2\\ 1 & -1 & 2 \end{array} \right] \left[ \begin{array}{cc} 1 & 1\\ -1 & -1\\ 2 & 2 \end{array} \right] = \left[ \begin{array}{cc} 6 & 6\\ 6 & 6 \end{array} \right]</tex> <tex>A^TA= \left[ \begin{array}{ccc} 1 & -1 & 2\\ 1 & -1 & 2 \end{array} \right] \left[ \begin{array}{cc} 1 & 1\\ -1 & -1\\ 2 & 2 \end{array} \right] = \left[ \begin{array}{cc} 6 & 6\\ 6 & 6 \end{array} \right]</tex>](lib/plugins/latex/images/ebf6733c5f934d6ee23a10f3f04a80fe892370c7_0.png)
Es claro que 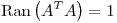 . Entonces
. Entonces  es aval de
es aval de 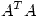 . Además:
. Además:
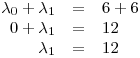
Luego, 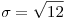 y entonces:
y entonces:
![<tex>A=\left[ \begin{array}{c} 1 \\ -1 \\ 2 \end{array} \right] \frac{\sqrt{12}}{\sqrt{2}\sqrt{6}} \left[ \begin{array}{cc} 1 & 1 \end{array} \right] = \left[ \begin{array}{c} 1 \\ -1 \\ 2 \end{array} \right] \left[ \begin{array}{cc} 1 & 1 \end{array} \right]</tex> <tex>A=\left[ \begin{array}{c} 1 \\ -1 \\ 2 \end{array} \right] \frac{\sqrt{12}}{\sqrt{2}\sqrt{6}} \left[ \begin{array}{cc} 1 & 1 \end{array} \right] = \left[ \begin{array}{c} 1 \\ -1 \\ 2 \end{array} \right] \left[ \begin{array}{cc} 1 & 1 \end{array} \right]</tex>](lib/plugins/latex/images/a9f118bbfb7f3d9485fd74aa6e50219d76d99ae1_0.png)
![<tex>A^\dagger = V_r \sigma^{-1} U_r^T = \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \frac{1}{\sqrt{12}\sqrt{2}\sqrt{6}} \left[ \begin{array}{ccc} 1 & -1 & 2 \end{array} \right] = \frac{1}{12} \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \left[ \begin{array}{ccc} 1 & -1 & 2 \end{array} \right]</tex> <tex>A^\dagger = V_r \sigma^{-1} U_r^T = \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \frac{1}{\sqrt{12}\sqrt{2}\sqrt{6}} \left[ \begin{array}{ccc} 1 & -1 & 2 \end{array} \right] = \frac{1}{12} \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \left[ \begin{array}{ccc} 1 & -1 & 2 \end{array} \right]</tex>](lib/plugins/latex/images/e96326398c9df4e00372318ed69db66360ec92cd_0.png)
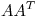 es matriz de proyección sobre Col(
es matriz de proyección sobre Col(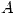 ) y además
) y además 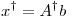 es solución de cuadrados mínimos de mínima norma, siendo el problema de cuadrados mínimos:
es solución de cuadrados mínimos de mínima norma, siendo el problema de cuadrados mínimos: 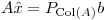
El cual es análogo a:
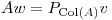
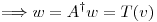
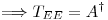
Punto 4
a)
Cambio de Nombres: llamo 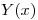 a
a 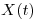 , y pues
, y pues 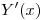 a
a 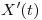
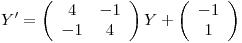
Homogéneo
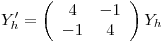
Como 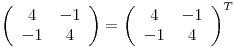 , es ortogonalmente diagonalizable:
, es ortogonalmente diagonalizable:
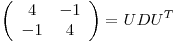
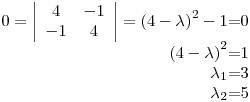
 y
y 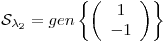
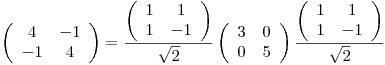
Cambio de Variables:

Queda, entonces:
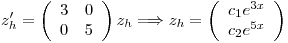
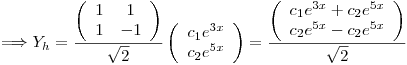
Particular
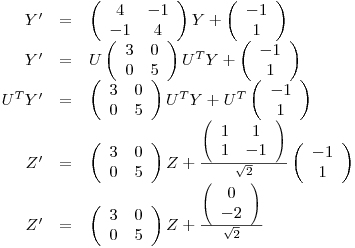
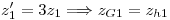 pues
pues 
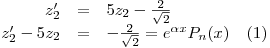
donde  y
y 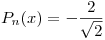
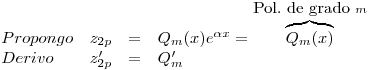
Reemplazo en 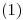 :
:
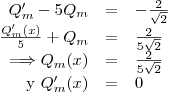
Pues si 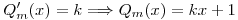 y
y 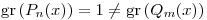
Entonces 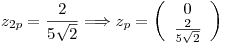
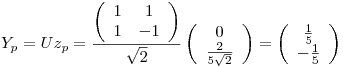
General
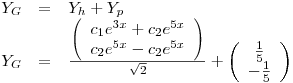
b)
Homogéneo
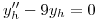
Planteo el polinomio fundamental asociado:
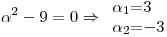

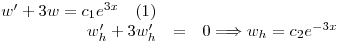
Propongo: 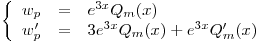
Reemplazo en 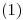 :
:
![<tex>\begin{array}{rcl} e^{3x} \left[ 3Q_m(x)+Q_m'+3Q_m(x) \right] &=& c_1 e^{3x}\\6Q_m(x)+Q_m'(x) &=& c_1, \qquad e^{3x} \neq 0 \quad \forall x \in \mathbf{R}\\\Longrightarrow Q_m(x) &=& \frac{c_1}{6} \end{array}</tex> <tex>\begin{array}{rcl} e^{3x} \left[ 3Q_m(x)+Q_m'+3Q_m(x) \right] &=& c_1 e^{3x}\\6Q_m(x)+Q_m'(x) &=& c_1, \qquad e^{3x} \neq 0 \quad \forall x \in \mathbf{R}\\\Longrightarrow Q_m(x) &=& \frac{c_1}{6} \end{array}</tex>](lib/plugins/latex/images/c483ff478126e37a90e760bdef34d65c6431c49a_0.png)
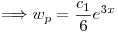
Entonces: 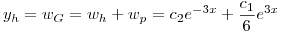
Particular
Propongo:
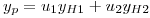 , y elijo
, y elijo  &
& 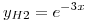
Queda:
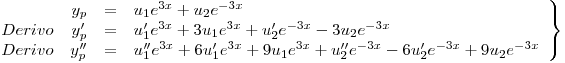 y reemplazo en
y reemplazo en 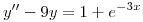
Reemplazando:
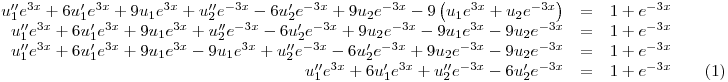
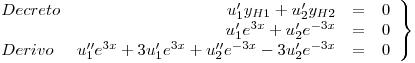 Reemplazo en
Reemplazo en 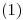
Reemplazando:
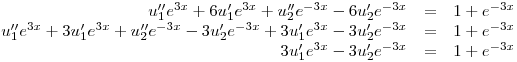
Queda:
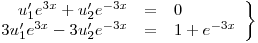 y es entonces
y es entonces 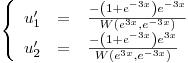
Donde
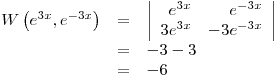
Con lo cual queda:
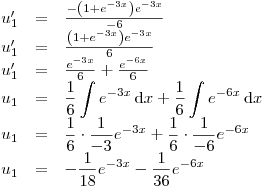
Y también:

Y entonces:
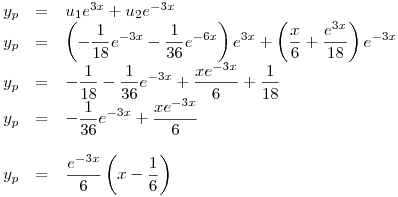
General
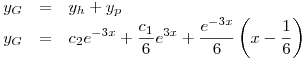
La condición es que sea finito lo siguiente:
![<tex>\begin{array}{rcl} \displaystyle \lim_{x\rightarrow+\infty} y_G &=& \displaystyle \lim_{x\rightarrow+\infty} \left[ \displaystyle c_2 e^{-3x} + \frac{c_1}{6} e^{3x} + \frac{e^{-3x}}{6} \left( x- \frac{1}{6} \right) \right]\\ &=& \displaystyle \lim_{x\rightarrow+\infty} \left[ \displaystyle c_2 e^{-3x} + \frac{c_1}{6} e^{3x} + \frac{x}{6e^{3x}} - \frac{e^{-3x}}{36} \right]\end{array}</tex> <tex>\begin{array}{rcl} \displaystyle \lim_{x\rightarrow+\infty} y_G &=& \displaystyle \lim_{x\rightarrow+\infty} \left[ \displaystyle c_2 e^{-3x} + \frac{c_1}{6} e^{3x} + \frac{e^{-3x}}{6} \left( x- \frac{1}{6} \right) \right]\\ &=& \displaystyle \lim_{x\rightarrow+\infty} \left[ \displaystyle c_2 e^{-3x} + \frac{c_1}{6} e^{3x} + \frac{x}{6e^{3x}} - \frac{e^{-3x}}{36} \right]\end{array}</tex>](lib/plugins/latex/images/fc20dd4ed361d0c190b2b3c69a26d615e3a8ea71_0.png)
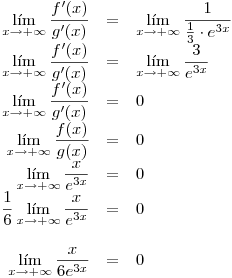
Veamos qué sucede con el tercer término. Allí tenemos una indeterminación del tipo 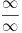 y para salvarla usaremos la regla de l'Hôpital:
y para salvarla usaremos la regla de l'Hôpital:
Llamemos 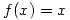 y
y 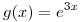 . Ambas son derivables en todo
. Ambas son derivables en todo  ,
, 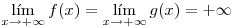 y además
y además 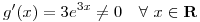 . Entonces: si existe
. Entonces: si existe 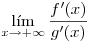 entonces existe
entonces existe 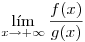 y además (por si fuera poco) son iguales.
y además (por si fuera poco) son iguales.
Ahora veamos qué sucede con el segundo término. Para que 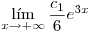 sea finito, debe ser necesariamente
sea finito, debe ser necesariamente 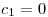 , ya que de otro modo el límite sería
, ya que de otro modo el límite sería 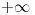 .
.
Nos queda, pues:
![<tex>\begin{array}{rcl} \displaystyle \lim_{x\rightarrow+\infty} y_G &=& \displaystyle \lim_{x\rightarrow+\infty} \left[ \displaystyle c_2 e^{-3x} + \frac{0}{6} e^{3x} + \frac{e^{-3x}}{6} \left( x- \frac{1}{6} \right) \right]\\ &=& \displaystyle \lim_{x\rightarrow+\infty} \left[ \displaystyle c_2 e^{-3x} + \frac{0}{6} e^{3x} + \frac{x}{6e^{3x}} - \frac{e^{-3x}}{36} \right]\\ &=& \displaystyle \lim_{x\rightarrow+\infty} \left( c_2 e^{-3x} \right) + \lim_{x\rightarrow+\infty} \left( \frac{0}{6} e^{3x} \right) + \lim_{x\rightarrow+\infty} \left( \frac{x}{6e^{3x}} \right) + \lim_{x\rightarrow+\infty} \left( - \frac{e^{-3x}}{36} \right)\\ &=& 0 + 0 + 0 + 0\\\displaystyle \lim_{x\rightarrow+\infty} y_G &=& 0\end{array}</tex> <tex>\begin{array}{rcl} \displaystyle \lim_{x\rightarrow+\infty} y_G &=& \displaystyle \lim_{x\rightarrow+\infty} \left[ \displaystyle c_2 e^{-3x} + \frac{0}{6} e^{3x} + \frac{e^{-3x}}{6} \left( x- \frac{1}{6} \right) \right]\\ &=& \displaystyle \lim_{x\rightarrow+\infty} \left[ \displaystyle c_2 e^{-3x} + \frac{0}{6} e^{3x} + \frac{x}{6e^{3x}} - \frac{e^{-3x}}{36} \right]\\ &=& \displaystyle \lim_{x\rightarrow+\infty} \left( c_2 e^{-3x} \right) + \lim_{x\rightarrow+\infty} \left( \frac{0}{6} e^{3x} \right) + \lim_{x\rightarrow+\infty} \left( \frac{x}{6e^{3x}} \right) + \lim_{x\rightarrow+\infty} \left( - \frac{e^{-3x}}{36} \right)\\ &=& 0 + 0 + 0 + 0\\\displaystyle \lim_{x\rightarrow+\infty} y_G &=& 0\end{array}</tex>](lib/plugins/latex/images/884a2621cceeaf46b36d675cff3fbf334dcddc42_0.png)
Y la única condición para ello es que  .
.
La ecuación que cumple con la condición pedida es, pues