Examen Final - 61.08. Álgebra II A - 29/02/2008
Cátedra: Única
Fecha: 2º Cuatrimestre 2007
Día: 29/02/2008
Enunciado
Problema 1
Sea 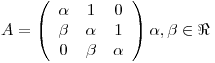
a) Hallar los valores de  y
y 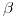 para los cuales existe una base de
para los cuales existe una base de 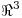 compuesta por autovectores de A.
compuesta por autovectores de A.
b) Considerar 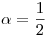 y
y 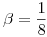 . Hallar todos los
. Hallar todos los 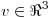 que satisfagan la condición:
que satisfagan la condición: ![<tex>\mathop {{\text{l\'i m}}}\limits_{k \to \infty } A^k v = \left[ {\begin{array}{*{20}c} 8 & 4 & 1 \\ \end{array} } \right]^t</tex> <tex>\mathop {{\text{l\'i m}}}\limits_{k \to \infty } A^k v = \left[ {\begin{array}{*{20}c} 8 & 4 & 1 \\ \end{array} } \right]^t</tex>](lib/plugins/latex/images/4e842b9592a61b72d4c8f08ee530f5ba9936861d_0.png)
Problema 2
a) Se sabe que 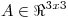 es diagonalizable ortogonalmente, que
es diagonalizable ortogonalmente, que ![<tex>\left[\begin{array}{ccc}2 & {-2} & {-1} \\\end{array}\right]^t</tex> <tex>\left[\begin{array}{ccc}2 & {-2} & {-1} \\\end{array}\right]^t</tex>](lib/plugins/latex/images/0a2338a204916a60c6994d701efe4e08f104b6c6_0.png) es autovector de A y que
es autovector de A y que ![<tex>A \left[\begin{array}{ccc}1 & 0 & 0 \\\end{array}\right]^t =\left[\begin{array}{ccc}3 & 2 & 2 \\\end{array}\right]^t</tex> <tex>A \left[\begin{array}{ccc}1 & 0 & 0 \\\end{array}\right]^t =\left[\begin{array}{ccc}3 & 2 & 2 \\\end{array}\right]^t</tex>](lib/plugins/latex/images/ca2843ee63057922786849446e1a77bc8c3957c2_0.png) y
y ![<tex>A \left[\begin{array}{ccc}0 & 1 & 0 \\\end{array}\right]^t =\left[\begin{array}{ccc}2 & 2 & 0 \\\end{array}\right]^t</tex> <tex>A \left[\begin{array}{ccc}0 & 1 & 0 \\\end{array}\right]^t =\left[\begin{array}{ccc}2 & 2 & 0 \\\end{array}\right]^t</tex>](lib/plugins/latex/images/9385db06ab55e2dd0ac1ef202fc5a20ee6b9a559_0.png) .
.
Hallar los autovalores de A y una base ortonormal de 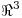 compuesta por autovectores de A.
compuesta por autovectores de A.
b) Sea 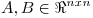 simétricas. Probar que si los autovalores de A pertenecen al intervalo [a,b] y los de B al intervalo [c,d], entonces los autovalores de A+B se encuentran en [a+c,b+d].
simétricas. Probar que si los autovalores de A pertenecen al intervalo [a,b] y los de B al intervalo [c,d], entonces los autovalores de A+B se encuentran en [a+c,b+d].
Problema 3
a) Sea 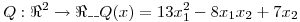 hallar todos los
hallar todos los  de norma 1 que verifiquen
de norma 1 que verifiquen 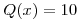 .
.
b) Sean 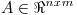 y
y 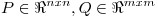 matrices ortogonales, probar que si
matrices ortogonales, probar que si 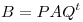 entonces
entonces 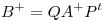 , donde
, donde 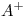 y
y 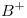 representan las matrices seudoinversas de moore-penrose de A y B respectivamente.
representan las matrices seudoinversas de moore-penrose de A y B respectivamente.
Problema 4
a) Sea 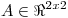 simétrica tal que
simétrica tal que 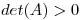 y
y 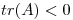 . Probar que toda solución
. Probar que toda solución 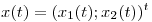 del sistema de ecuaciones
del sistema de ecuaciones 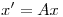 verifica
verifica 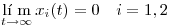 .
.
b) Hallar todas las soluciones de la ecuación:  (sugerencia: considere
(sugerencia: considere 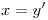 ).
).
Resolución
