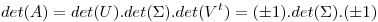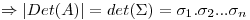Examen (Final) - 61.08. Algebra II - 20/02/2008
Cátedra: Indistinta.
Fecha: 3ra Oportunidad - Verano 2008
Día: 20/02/2008
Punto 1
(a) Sea 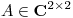 que posee dos autovalores distintos. Probar que si
que posee dos autovalores distintos. Probar que si 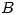 es tal que
es tal que  entonces
entonces 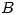 es diagonalizable. (Sugerencia: considere a
es diagonalizable. (Sugerencia: considere a 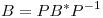 )
)
(b)Sea 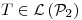 definida por:
definida por: 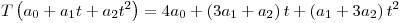
Probar que no existe una base 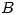 de
de 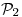 tal que:
tal que:
![<tex>[T]_B = \left[ \begin{array}{c c c}3 & 1 & 0\\-1 & 5 & 0\\0 & 0 & 2\\\end{array} \right]</tex> <tex>[T]_B = \left[ \begin{array}{c c c}3 & 1 & 0\\-1 & 5 & 0\\0 & 0 & 2\\\end{array} \right]</tex>](lib/plugins/latex/images/50f424371ce48fdce4d2b01a2ee40aca8c6efcb0_0.png)
Punto 2
(a) Sea 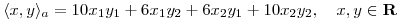
Probar que 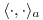 es producto interno en
es producto interno en 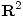 y hallar
y hallar 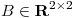 simétrica e indefinida tal que
simétrica e indefinida tal que 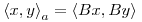 cuando
cuando 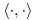 es el PI canónico de
es el PI canónico de 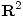 .
.
(b) Graficar el conjunto 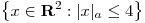 y hallar
y hallar 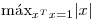 y los vectores donde alcanza extremo.
y los vectores donde alcanza extremo.
Punto 3
(a) Sea 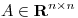 probar que
probar que 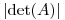 es igual al producto de los valores singulares de
es igual al producto de los valores singulares de 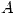 .
.
(b) Hallar 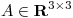 tal que
tal que 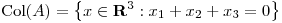 y
y 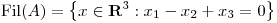 y 3 y 2 son valores singulares de
y 3 y 2 son valores singulares de 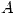 .
.
Punto 4
(a) Probar que toda solución 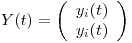 del sistema:
del sistema:
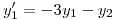
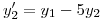
Satisface la condición 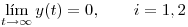
(b) Resolver el problema de valores iniciales 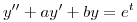 ,
, 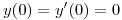 .
.
Sabiendo que 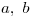 son constantes reales y que
son constantes reales y que 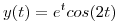 es solución de la ecuación homogénea asociada.
es solución de la ecuación homogénea asociada.
Resolucion
Punto 1
(a)
A es una matriz 2×2 (aunque si fuese n X n la idea sería la misma) con 2 autovalores distintos. Entonces A es diagonalizable y se puede escribir 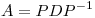 con
con ![<tex> D=\left [ \begin{array}{rr} \lambda_1 & 0\\ 0 & \lambda_2 \end{array} \right ] </tex> <tex> D=\left [ \begin{array}{rr} \lambda_1 & 0\\ 0 & \lambda_2 \end{array} \right ] </tex>](lib/plugins/latex/images/2526e8a53ffcbbc7b2b3233ea39c02d562cd3747_0.png) con
con 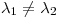 .
.
Ahora escribimos 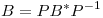 (lo cual es siempre posible tomando
(lo cual es siempre posible tomando 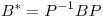 ). Si probamos que
). Si probamos que 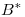 es diagonal, entonces
es diagonal, entonces 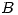 es diagonalizable.
es diagonalizable.
Como  , tenemos que
, tenemos que
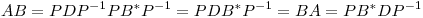
con lo cual
 , y, por lo tanto, cancelando
, y, por lo tanto, cancelando 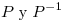 resulta
resulta
 . Ahora usamos que
. Ahora usamos que 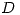 es diagonal y que los elementos de la diagonal son distintos. Llamando
es diagonal y que los elementos de la diagonal son distintos. Llamando 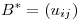 , tenemos
, tenemos
![<tex> \left [ \begin{array}{rr} \lambda_1 & 0\\ 0 & \lambda_2 \end{array} \right ] \left [ \begin{array}{rr} u_{11} & u_{12}\\ u_{21} & u_{22} \end{array} \right ] = \left [ \begin{array}{rr} \lambda_1 u_{11}& \lambda_1 u_{12}\\ \lambda_2 u_{21} & \lambda_2 u_{22}\end{array} \right ] </tex> <tex> \left [ \begin{array}{rr} \lambda_1 & 0\\ 0 & \lambda_2 \end{array} \right ] \left [ \begin{array}{rr} u_{11} & u_{12}\\ u_{21} & u_{22} \end{array} \right ] = \left [ \begin{array}{rr} \lambda_1 u_{11}& \lambda_1 u_{12}\\ \lambda_2 u_{21} & \lambda_2 u_{22}\end{array} \right ] </tex>](lib/plugins/latex/images/85b53035d05f108c237f97b7296db175bbab4fa0_0.png)
y
![<tex> \left [ \begin{array}{rr} u_{11} & u_{12}\\ u_{21} & u_{22} \end{array} \right ] \left [ \begin{array}{rr} \lambda_1 & 0\\ 0 & \lambda_2 \end{array} \right ] = \left [ \begin{array}{rr} \lambda_1 u_{11}& \lambda_2 u_{12}\\ \lambda_1 u_{21} & \lambda_2 u_{22}\end{array} \right ] </tex> <tex> \left [ \begin{array}{rr} u_{11} & u_{12}\\ u_{21} & u_{22} \end{array} \right ] \left [ \begin{array}{rr} \lambda_1 & 0\\ 0 & \lambda_2 \end{array} \right ] = \left [ \begin{array}{rr} \lambda_1 u_{11}& \lambda_2 u_{12}\\ \lambda_1 u_{21} & \lambda_2 u_{22}\end{array} \right ] </tex>](lib/plugins/latex/images/6247c9b00a1415c836cde7667a11a4f228163048_0.png) .
.
Entonces  y
y  . Como
. Como 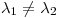 , necesariamente
, necesariamente  y
y
 , con lo cual
, con lo cual 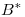 es diagonal.
es diagonal.
(b)
Punto 2
(a)
Si 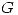 es la matriz definida positiva de p.i que cumple
es la matriz definida positiva de p.i que cumple
 , entonces
, entonces
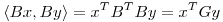 .
Como la matriz que buscamos es simétrica, la igualdad se cumple si hallamos
.
Como la matriz que buscamos es simétrica, la igualdad se cumple si hallamos 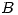 simétrica e indefinida tal que
simétrica e indefinida tal que  .
.
Para hallar 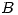 , diagonalizamos ortogonalmente
, diagonalizamos ortogonalmente 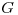 ,
, 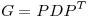 . Teniendo en cuenta que los avas de
. Teniendo en cuenta que los avas de 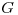 son positivos (por ser definida positiva), definimos
son positivos (por ser definida positiva), definimos 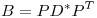 con
con 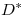 una matriz diagonal en la cual aparecen las raíces cuadradas de los elementos de
una matriz diagonal en la cual aparecen las raíces cuadradas de los elementos de  , una con signo positivo y otra con signo negativo. Tal
, una con signo positivo y otra con signo negativo. Tal 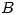 es simétrica, indefinida y verifica
es simétrica, indefinida y verifica  .
.
(b)
Punto 3
(a)