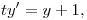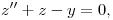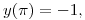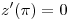Examen (Final) - 61.08. Algebra II - 12/02/2008
Cátedra: Única
Fecha: 2da Oportunidad - Verano 2008
Día: 12/02/2008
Punto 1
Sea base 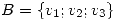 de un
de un  - espacio vectorial
- espacio vectorial  y sea
y sea 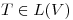 definida por:
definida por:
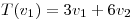
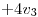
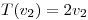
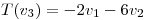
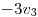
(a) Hallar tres subespacios de dimension 1, 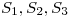 tales que:
tales que:
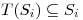 para
para 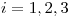 y
y 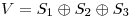
(b) Hallar ![<tex>[ T^k ]_B</tex> <tex>[ T^k ]_B</tex>](lib/plugins/latex/images/0b0e1e6930350ddba67d37a57495f7206c993be7_0.png) para
para 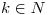
Punto 2
(a) Hallar 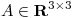 simétrica tal que
simétrica tal que ![<tex> [1 \quad 1 \quad 0]^t </tex> <tex> [1 \quad 1 \quad 0]^t </tex>](lib/plugins/latex/images/e4f2c541b09e983c341d51d657209d285b7d3e90_0.png) y
y ![<tex>[0 \quad 1 \quad 1]^t</tex> <tex>[0 \quad 1 \quad 1]^t</tex>](lib/plugins/latex/images/f538d40d072edef2f800b28e4a66e5638a203ebe_0.png) sean autovectores de
sean autovectores de  ,
, 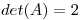 y
y 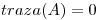 .
.
(b) Sea 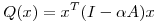 con
con  la matriz hallada en (a) y
la matriz hallada en (a) y 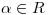 . Hallar
. Hallar 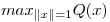 y todos los vectores en los cuales se alcanza ese extremo.
y todos los vectores en los cuales se alcanza ese extremo.
Punto 3
(a) Sea 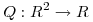 ,
, 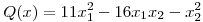 . Hallar todos los
. Hallar todos los 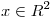 de norma 1 tales que
de norma 1 tales que 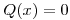
(b) Sea 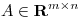 com m valores singulares no nulos. Probar que
com m valores singulares no nulos. Probar que 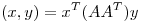 es producto interno en
es producto interno en 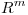 .
.
Punto 4
(a) Sea  una matriz n x n. Probar que si
una matriz n x n. Probar que si  posee n autovalores distintos entonces existe una matriz inversible
posee n autovalores distintos entonces existe una matriz inversible  tal que el cambio de variables
tal que el cambio de variables 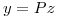 transforma el sistema de ecuaciones diferenciales
transforma el sistema de ecuaciones diferenciales 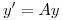 en el sistema
en el sistema 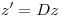 con
con  una matriz diagonal.
una matriz diagonal.
(b) Hallar todas las funciones 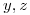 que satisfagan las condiciones:
que satisfagan las condiciones: