Examen Final - 61.08. Álgebra II
Cátedra: Todas
Fecha: 5º Oportunidad - (1º Cuatrimestre|Invierno) 2007
Día: 8/08/2007
Punto I
(a) Sea 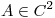 diagonalizable. Probar que
diagonalizable. Probar que 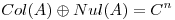 .
.
(b) Hallar los autovalores y autoespacios de 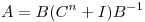 con
con ![<tex>B= \left[ \begin{array}{ccc} 1 & -1 & 0\\ -2 & 1 & 1 \\ 0 & 1 & 2\\ \end{array} \right]</tex> <tex>B= \left[ \begin{array}{ccc} 1 & -1 & 0\\ -2 & 1 & 1 \\ 0 & 1 & 2\\ \end{array} \right]</tex>](lib/plugins/latex/images/7d61578d722c270ba8a5eb968243df69cb111e66_0.png) y
y ![<tex>C= \left[ \begin{array}{ccc} 2 & -1 & 0\\ -1 & 2 & 0\\ -1 & 1 & 2\\ \end{array} \right]</tex> <tex>C= \left[ \begin{array}{ccc} 2 & -1 & 0\\ -1 & 2 & 0\\ -1 & 1 & 2\\ \end{array} \right]</tex>](lib/plugins/latex/images/3405529d1311209fe80c7760d18dd43a4cb9c9ce_0.png)
Punto II
(a) Probar que si 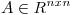 es simétrica y sus autovlaores tienen módulo 1 entonces las comlumnas de A forman una BOG de
es simétrica y sus autovlaores tienen módulo 1 entonces las comlumnas de A forman una BOG de 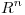 .
.
(b) Sabiendo que Q(x) es una forma cuadrática en 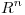 tal que con el cambio
tal que con el cambio 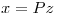 con
con 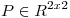 ortogonal, se transforma en
ortogonal, se transforma en 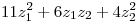 , hallar
, hallar  y
y 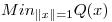 .
.
Punto III
(a) Sea 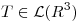 definida por
definida por ![<tex>T(x)= \left[ \begin{array}{c} x_1+x_2-x_3\\ x_1+ \alpha x_2-x_3\\ x_2+2x_3\\ \end{array} \right]</tex> <tex>T(x)= \left[ \begin{array}{c} x_1+x_2-x_3\\ x_1+ \alpha x_2-x_3\\ x_2+2x_3\\ \end{array} \right]</tex>](lib/plugins/latex/images/5d2225d598a7c876792028c97d91ac9ca9242b24_0.png) . Determinar para qué valores de
. Determinar para qué valores de 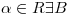 y
y  ortonormales de
ortonormales de 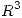 tal que
tal que ![<tex>[T]_{BC}= \left[ \begin{array}{ccc} \gamma _1 & 0 & 0\\ 0 & \gamma _2 & 0\\ 0 & 0 & 0\\ \end{array} \right]</tex> <tex>[T]_{BC}= \left[ \begin{array}{ccc} \gamma _1 & 0 & 0\\ 0 & \gamma _2 & 0\\ 0 & 0 & 0\\ \end{array} \right]</tex>](lib/plugins/latex/images/2ad0ffbbb75db3f42976e4b4a2f663b53a748620_0.png) con
con 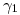 y
y 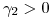 . Para los valores de
. Para los valores de  hallados mostrar esas bases.
hallados mostrar esas bases.
(b) Probar que  con
con 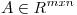 .
.
Punto IV
(a) Expresar en términos de funciones reales la solución general de ![<tex>Y'= \left[ \begin{array}{cccc} 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ \end{array} \right]Y</tex> <tex>Y'= \left[ \begin{array}{cccc} 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ \end{array} \right]Y</tex>](lib/plugins/latex/images/c6054c820d4015d8cf4ab35edc3051736bd189f3_0.png) .
.
(b) Sea 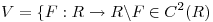 y
y 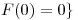 y sea
y sea  definida como
definida como 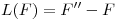 . Probar que
. Probar que  es transformación lineal, hallar bases de
es transformación lineal, hallar bases de 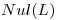 y todas las
y todas las 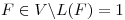 .
.
