Tabla de Contenidos
Examen Final - 61.08. Álgebra II
Cátedra: Todas
Fecha: 4º Oportunidad - (1º Cuatrimestre|Invierno) 2007
Día: 31/07/2007
Punto I
(a) Sean A y B matrices de 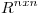 tal que A es diagonalizable y todo autovector de A es a la vez autovector de B. Probar que
tal que A es diagonalizable y todo autovector de A es a la vez autovector de B. Probar que  .
.
(b) Sea ![<tex>A= \left[ \begin{array}{cc} -1/2 & 3\\ -1/2 & 2 \\ \end{array} \right]</tex> <tex>A= \left[ \begin{array}{cc} -1/2 & 3\\ -1/2 & 2 \\ \end{array} \right]</tex>](lib/plugins/latex/images/fab2e255aadfd203f2ed51f3fee872484fcc1bbf_0.png) . Hallar todos los
. Hallar todos los 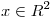 tales que
tales que ![<tex>\lim_{k \to \infty} (A^kx)= \left[ \begin{array}{c} 2\\ 1\\ \end{array} \right]</tex> <tex>\lim_{k \to \infty} (A^kx)= \left[ \begin{array}{c} 2\\ 1\\ \end{array} \right]</tex>](lib/plugins/latex/images/d67b499e41e4343f06457e2268cd1f08299396dc_0.png) .
.
Punto II
Sea ![<tex>Q(x)=x^T \left[ \begin{array}{cc} a & b\\ b & a\\ \end{array} \right]x</tex> <tex>Q(x)=x^T \left[ \begin{array}{cc} a & b\\ b & a\\ \end{array} \right]x</tex>](lib/plugins/latex/images/c38268392d704994e6321b001f801021ffea6086_0.png) , a y b reales y positivos.
, a y b reales y positivos.
(a) Graficar el conjunto de pares 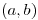 para los cuales se cumple
para los cuales se cumple 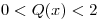
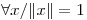 .
.
(b) Tomando 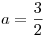 y
y 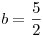 , graficar
, graficar 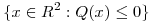 .
.
Punto III
(a) Probar que si 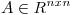 tal que
tal que 
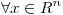 entonces los valores singulares de A son todos 1 y es ortogonal.
entonces los valores singulares de A son todos 1 y es ortogonal.
(b) Hallar 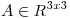 tal que
tal que ![<tex>P= \left[ \begin{array}{cc} 1/2 & 1/2\\ 1/2 & 1/2 \\ \end{array} \right]</tex> <tex>P= \left[ \begin{array}{cc} 1/2 & 1/2\\ 1/2 & 1/2 \\ \end{array} \right]</tex>](lib/plugins/latex/images/6ed4e41c74cec092ece66aab187b6d557ae07193_0.png) proyecte sobre
proyecte sobre 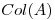 ;
; 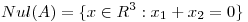 y
y 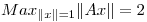 .
.
Punto IV
(a) Resolver el siguiente sistema de ecuaciones:
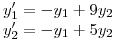
(b) Hallar los valores de 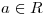 para que toda solución
para que toda solución  de la ecuación
de la ecuación 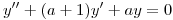 tenga límite finito cuando
tenga límite finito cuando 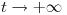 .
.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
