Examen Final - 61.08. Álgebra II
Cátedra: Todas
Fecha: 3º Oportunidad - (1º Cuatrimestre|Invierno) 2007
Día: 23/07/2007
Enunciado
Punto I
(a) Dada ![<tex>A= \left[ \begin{array}{ccc} 0 & 0 & b\\ 1 & 0 & 1\\ 0 & 1 & a\\ \end{array} \right]</tex> <tex>A= \left[ \begin{array}{ccc} 0 & 0 & b\\ 1 & 0 & 1\\ 0 & 1 & a\\ \end{array} \right]</tex>](lib/plugins/latex/images/f2904de364259f285f1169ab26c4f210484a60e8_0.png) halle los valores de a y b para que 1 sea autovalor de A y A no sea semejante a una matriz diagonal.
halle los valores de a y b para que 1 sea autovalor de A y A no sea semejante a una matriz diagonal.
(b) Sea 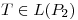 tal que
tal que ![<tex>[T]_E=A</tex> <tex>[T]_E=A</tex>](lib/plugins/latex/images/81fd39227eaec8be104ce3e8d2af01f7d3246dc8_0.png) con
con 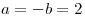 y
y 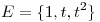 . Halle
. Halle 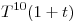 .
.
Punto II
Sea 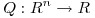 ;
; 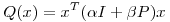 con
con 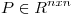 matriz de proyección y
matriz de proyección y  y
y 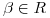 .
.
(a) Halle los valores de  y
y 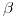 para que
para que 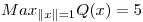 y
y 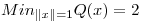 .
.
(b) Suponiendo  y
y  y
y 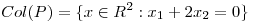 grafique el conjunto
grafique el conjunto 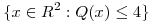 .
.
Punto III
(a) Demostrar que si 4 es valor singular de 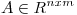 , entonces existe
, entonces existe 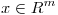 con
con  tal que
tal que 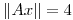 .
.
(b) Probar que dada 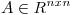 con
con 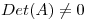 siempre puede hallarse una matriz ortogonal
siempre puede hallarse una matriz ortogonal 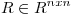 de modo tal que
de modo tal que 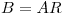 sea simétrica y definida positiva.
sea simétrica y definida positiva.
Punto IV
(a) Hallar la solución general del sistema de ecuaciones
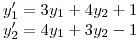
(b) Halle la solución a valores iniciales de 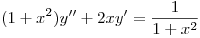 ,
, 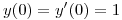 . Pista: considere
. Pista: considere 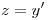 .
.
Resolución
Punto III
a)Hago una DVS de A:
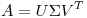 .
.
Tengo como dato que 4 es valor singular, entonces defino 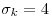
Tengo que demostrar que existe un x que cumpla 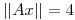 , o lo que es lo mismo
, o lo que es lo mismo 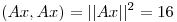 , con
, con 
Desarrollo el producto 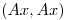 con la DVS de
con la DVS de  :
:
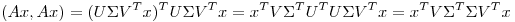
Sabiendo qeu 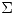 es una matriz definida por bloques,
es una matriz definida por bloques, 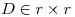 con
con 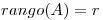 :
:
![<tex>\Sigma = \left[ \begin{array}{cc} D & 0 \\ 0 & 0 \\ \end{array} \right]</tex> <tex>\Sigma = \left[ \begin{array}{cc} D & 0 \\ 0 & 0 \\ \end{array} \right]</tex>](lib/plugins/latex/images/d1de68d2ce6b5489b08ac31bc96496de2b93e832_0.png)
![<tex>\Sigma^T \Sigma = \left[ \begin{array}{cc} D^2 & 0 \\ 0 & 0 \\ \end{array} \right]</tex> <tex>\Sigma^T \Sigma = \left[ \begin{array}{cc} D^2 & 0 \\ 0 & 0 \\ \end{array} \right]</tex>](lib/plugins/latex/images/148ea182cb74fd01dbb46ee01639e628fe4c0013_0.png)
Planteo tambein el cambio de variables ortogonal 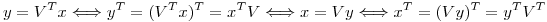
Entonces la expresión me queda:
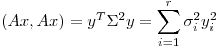
Propongo un  de manera tal que
de manera tal que 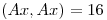 y
y

Se ve facil que el vector  con un
con un  en la k-ésima posición y ceros en las otras cumple ambas condiciones. Para obtener el x utilizamos la igualdad
en la k-ésima posición y ceros en las otras cumple ambas condiciones. Para obtener el x utilizamos la igualdad 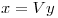
b) Hago una DVS de A:
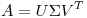 .
Entonces me queda
.
Entonces me queda 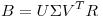 .
Para que B sea simétrica, se debe cumplir:
.
Para que B sea simétrica, se debe cumplir: 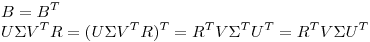
De aca obtenemos la condición 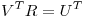 . En este caso
. En este caso 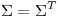 por ser una matriz cuadrada, ya que
por ser una matriz cuadrada, ya que 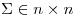 .
.
Se puede ver también que se comprueba que  es ortogonal, porque es producto de dos matrices ortogonales, siendo
es ortogonal, porque es producto de dos matrices ortogonales, siendo 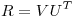 .
Ahora faltaría probar que B es definida positiva. Armo la siguiente forma cuadrática:
.
Ahora faltaría probar que B es definida positiva. Armo la siguiente forma cuadrática:
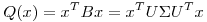
Realizo un cambio de variables 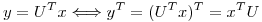
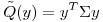
Para probar que esta forma cuadrática es definida positiva alcanzaria con ver que los elementos de la diagonal, es decir, los valores singulares, son estrictamente mayores que 0. Pero, sabemos que 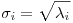 siendo
siendo 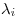 el i-ésimo autovalor de
el i-ésimo autovalor de 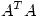 , pero como
, pero como 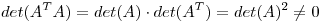 , 0 no puede ser autovalor, entonces 0 tampoco puede ser valor singular, y queda demostrado que siempre existe
, 0 no puede ser autovalor, entonces 0 tampoco puede ser valor singular, y queda demostrado que siempre existe  que cumpla las condiciones requeridas
que cumpla las condiciones requeridas
