Examen Final - [61.08] Álgebra II - 13/7/07
Cátedra: Todas
Fecha: 2º Oportunidad - 1º Cuatrimestre 2007
Día: 13/07/2007
Enunciado
Punto 1
Sea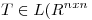 
), definida por 
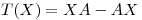, con 
.
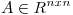(a) Demostrar que 0 es autovalor de 
.
(b) Considerando ![<tex> A= \left[ \begin{array}{cc} 2 & 1 \\ 1 & 2 \\ \end{array} \right] </tex>](lib/plugins/latex/images/fd843b9760deb01c4d5a1ffe39b5a23075cda6f5_0.png "<tex> A= \left[ \begin{array}{cc} 2 & 1 \\ 1 & 2 \\ \end{array} \right] </tex>")
, hallar, si existe una base 
de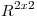 
tal que ![<tex> [T]_B </tex>](lib/plugins/latex/images/c05d7a3a8bd3c076ce6c4bc7acdd9ebe2d6079e3_0.png "<tex> [T]_B </tex>")
sea diagonal.
Punto 2
(a) Dada la forma cuadrática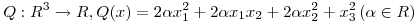 
, hallar 
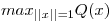y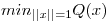 
.
(b) Sea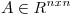 
simétrica y tal que 
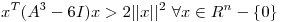. Demostrar que existe 
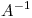y que todos los autovalores de 
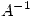se encuentran en el intervalo 
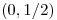. (Sugerencia: 
)
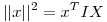Punto 3
(a) Sea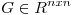 
tal que 
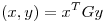es producto interno en 
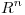y sea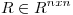 
ortogonal. Probar que los autovalores de 
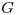coinciden con los valores singulares de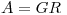 
(b) Sea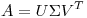 
una descomposición en valores singulares de 
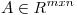. Probar que cada columna de 
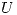es autovector de 
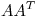y que los cuadrados de los elementos no nulos de 
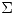son autovalores de .
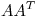Punto 4
(a) Hallar todas las funciones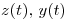 
que satisfacen las condiciones.
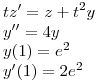
(b) Sabiendo que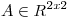 
es simétrica y tal que ![<tex>A[1 \, 2]^T = [2 \, 4]^T</tex>](lib/plugins/latex/images/1fc81778c0edd17fb91d9fc57af6b23f30e48302_0.png "<tex>A[1 \, 2]^T = [2 \, 4]^T</tex>")
y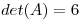 
, hallar la solución del problema a valor inicial ![<tex> X'=A^{-1}X, \, X(0) = [0 \, 1]^T </tex>](lib/plugins/latex/images/bb180e0102fb136fb98d5b71972be7e3ec4f48ce_0.png "<tex> X'=A^{-1}X, \, X(0) = [0 \, 1]^T </tex>")
Resolución
