Enunciado
1) Sea  y sea
y sea 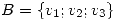 una base de
una base de  . (a) Sea
. (a) Sea 
![<tex>[f]_{B} = \left[ \begin{array}{ccc} 3 & 1 & 0 \\ 1 & 3 & 0 \\ 2\alpha-1 & 2\alpha-1 & 4 \end{array} \right]</tex> <tex>[f]_{B} = \left[ \begin{array}{ccc} 3 & 1 & 0 \\ 1 & 3 & 0 \\ 2\alpha-1 & 2\alpha-1 & 4 \end{array} \right]</tex>](lib/plugins/latex/images/c880e6731ea360f82e0a7bc3b11b43957192be03_0.png) , determine los valores de
, determine los valores de 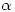 . para los cuales
. para los cuales ![<tex>[f]_B</tex> <tex>[f]_B</tex>](lib/plugins/latex/images/500a6475c38ca7e8d38f1dc35d00d864767a2935_0.png) es diagonalizable. Hallar los autovalores y autoespacios.
es diagonalizable. Hallar los autovalores y autoespacios.
(b) Considerando 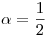 buscar la imagen de
buscar la imagen de  con
con 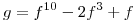 .
.
2) (a) Los valores del potencial eléctrico en el punto ![<tex> [x_1 \quad x_2]^t </tex> <tex> [x_1 \quad x_2]^t </tex>](lib/plugins/latex/images/b6609ab918cb92fbe691b025e2ce8a5370a46848_0.png) están dados por
están dados por 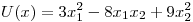 . Hallar las curvas equipotenciales y dibujar algunas.
. Hallar las curvas equipotenciales y dibujar algunas.
(b) Considerando la forma 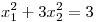 , hallar los puntos en los cuales el potencial es mínimo.
, hallar los puntos en los cuales el potencial es mínimo.
3) (a) Sea ![<tex> A = \left[ \begin{array}{ccc} -1 & 1 \\ 1 & 1 \\ -1 & 1 \\ 1 & 1 \\\end{array} \right]</tex> <tex> A = \left[ \begin{array}{ccc} -1 & 1 \\ 1 & 1 \\ -1 & 1 \\ 1 & 1 \\\end{array} \right]</tex>](lib/plugins/latex/images/d187f78cfe59392df59407883d037bae2bbee750_0.png)
![<tex>\left[ \begin{array}{ccc} \gamma_1 & 0 \\ 0 & \gamma_2 \\\end{array} \right]</tex> <tex>\left[ \begin{array}{ccc} \gamma_1 & 0 \\ 0 & \gamma_2 \\\end{array} \right]</tex>](lib/plugins/latex/images/fd47fd9fcf110cb0898bf2442dbc402302330ad1_0.png)
![<tex>\left[ \begin{array}{ccc} 4 & -3 \\ 3 & 4 \\\end{array} \right]</tex> <tex>\left[ \begin{array}{ccc} 4 & -3 \\ 3 & 4 \\\end{array} \right]</tex>](lib/plugins/latex/images/b38056bb7473d392025ea7bbbcc92fb69dc795e1_0.png) ,
,
Hallar una DVS y las matrices de proyección del 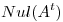 y
y 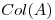
(b) Con  y
y 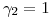 , busque todos los
, busque todos los  tales que
tales que 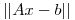 resulte mínimo.
resulte mínimo.
4) (a) Hallar la solución de la ecuación diferencial a valores iniciales de
![<tex> X' = \left[ \begin{array}{ccc} 1 & \alpha \\ \alpha & 1 \\\end{array} \right]X</tex> <tex> X' = \left[ \begin{array}{ccc} 1 & \alpha \\ \alpha & 1 \\\end{array} \right]X</tex>](lib/plugins/latex/images/4d46ca24c9b35bb6b0b7866bd778f843611223c8_0.png) ,
,
![<tex> X(0) = \left[ \begin{array}{ccc} 1 \\ 3 \\\end{array} \right]</tex> <tex> X(0) = \left[ \begin{array}{ccc} 1 \\ 3 \\\end{array} \right]</tex>](lib/plugins/latex/images/bed0831cf21877e4f6abb39b81fbb986b8db1d7e_0.png)
(b) Hallar la solución general de 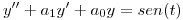 sabiendo que la solución de la ecuación diferencial homogénea asociada es
sabiendo que la solución de la ecuación diferencial homogénea asociada es 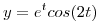
El examen se aprueba resolviendo correctamente al menos cuatro puntos. Justifique todas sus respuestas.
