Coloquio 21/12/2005
Enunciado
1) Sea  y sea
y sea 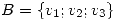 una base de
una base de  . (a) Sabiendo que para cierta base
. (a) Sabiendo que para cierta base 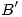 de
de  ,
,
![<tex>[T]_{B'} = \left[ \begin{array}{ccc} -1 & 0 & 0 \\ 0 & 1 & 0 \\0 & 1 & \alpha + 1 \end{array} \right]</tex> <tex>[T]_{B'} = \left[ \begin{array}{ccc} -1 & 0 & 0 \\ 0 & 1 & 0 \\0 & 1 & \alpha + 1 \end{array} \right]</tex>](lib/plugins/latex/images/dd4ec34b5e37bdec6da45adb4b3a2828d3831b0d_0.png) , determine los valores de
, determine los valores de 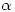 . para los cuales
. para los cuales ![<tex>[T]_B</tex> <tex>[T]_B</tex>](lib/plugins/latex/images/77974c5d33422dda29ab8c19452e9cbe246a3fa1_0.png) es diagonalizable.
es diagonalizable.
(b) Considerando 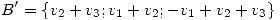 y
y 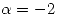 , hallar los autovalores y autoespacios de
, hallar los autovalores y autoespacios de 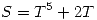 .
.
2) (a) Sea 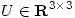 ortogonal y tal que
ortogonal y tal que 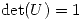 . Probar que existe
. Probar que existe 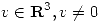 , tal que
, tal que 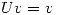 .
(b) Probar que si
.
(b) Probar que si 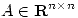 es simétrica y tal que
es simétrica y tal que 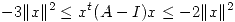 para todo
para todo 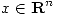 , entonces
, entonces  es inversible y los autovalores de
es inversible y los autovalores de 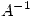 pertenecen al intervalo
pertenecen al intervalo ![<tex>[-1,\;-0.5]</tex> <tex>[-1,\;-0.5]</tex>](lib/plugins/latex/images/e2e5028e9764c4afcabe8167e6aaa5bd03050817_0.png)
3) La temperatura del punto ![<tex> [x_1 \quad x_2]^t </tex> <tex> [x_1 \quad x_2]^t </tex>](lib/plugins/latex/images/b6609ab918cb92fbe691b025e2ce8a5370a46848_0.png) del plano es
del plano es 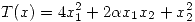
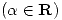 .
(a)Hallar los valores de
.
(a)Hallar los valores de 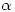 para los cuales las isotermas son curvas cerradas.
(b) Considerando
para los cuales las isotermas son curvas cerradas.
(b) Considerando  , hallar los puntos de la curva
, hallar los puntos de la curva 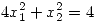 en los cuales la temperatura es máxima.
en los cuales la temperatura es máxima.
4) (a) Hallar 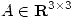 tal que 9 y 4 sean autovalores de
tal que 9 y 4 sean autovalores de 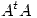 ,
, ![<tex> [0 \quad 1 \quad -1]^t \in \mathrm{Nul} (A) </tex> <tex> [0 \quad 1 \quad -1]^t \in \mathrm{Nul} (A) </tex>](lib/plugins/latex/images/0fa2f07be2b798260bf8a30545e9a4269443e661_0.png) y
y ![<tex> [-1 \quad 0 \quad 1]^t \in \mathrm{Nul} (A^t)</tex> <tex> [-1 \quad 0 \quad 1]^t \in \mathrm{Nul} (A^t)</tex>](lib/plugins/latex/images/3876a3d5b0c458847d1e485855480b5f101b3fff_0.png) .
.
(b) Sabiendo que 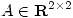 es simétrica y tal que
es simétrica y tal que ![<tex>A[2\quad 1]^t = [4 \quad 2]^t </tex> <tex>A[2\quad 1]^t = [4 \quad 2]^t </tex>](lib/plugins/latex/images/6b0475faad3bf80edd6af55d06e57612c8ad2ec2_0.png) y
y 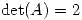 , hallar la solución del problema a valor inicial
, hallar la solución del problema a valor inicial 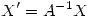 ,
, ![<tex>X(0) = [0 \quad 1 ]^t</tex> <tex>X(0) = [0 \quad 1 ]^t</tex>](lib/plugins/latex/images/724f0568c7ea7785fb6872e140b84c7a3bb3de84_0.png) .
.
Los alumnos del 2do cuatrimestre de 2004 o del 1ro de 2005 deben reemplazar el punto 4(b) por el siguiente:
(b*) Sea 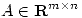 . Probar que
. Probar que 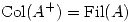 y que
y que 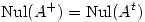 .
.
El examen se aprueba resolviendo correctamente al menos cuatro puntos. Justifique todas sus rerspuestas.
Resolución Ejercicio 1)
Resolución Ejercicio 2)
(b)
Si entonces
entonces 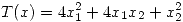 / con la restricción de que
/ con la restricción de que 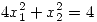
Primero voy a cambiar la restricción para que me quede de 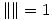
 entonces tengo que aplicar una transformación
entonces tengo que aplicar una transformación 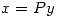 donde
donde  y
y 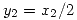
Planteo 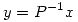 con
con
![<tex>P^{-1} = \left[ \begin{array}{ccc} 1 & 0 \\ 0 & 1/2 \\\end{array} \right]</tex> <tex>P^{-1} = \left[ \begin{array}{ccc} 1 & 0 \\ 0 & 1/2 \\\end{array} \right]</tex>](lib/plugins/latex/images/2f952ed07f416b52dc314972dd5ae57147f00202_0.png)
Quedaria:
![<tex> \left[ \begin{array}{ccc} y_1 \\y_2 \\\end{array} \right]</tex> <tex> \left[ \begin{array}{ccc} y_1 \\y_2 \\\end{array} \right]</tex>](lib/plugins/latex/images/2b72f7c1e0f7468b6a9299c7a212aed7e2cc7d09_0.png) =
=![<tex> \left[ \begin{array}{ccc} 1 & 0 \\ 0 & 1/2 \\\end{array} \right]</tex> <tex> \left[ \begin{array}{ccc} 1 & 0 \\ 0 & 1/2 \\\end{array} \right]</tex>](lib/plugins/latex/images/6783c2395b68699f0c2373d6b41d77d346cd63d6_0.png)
![<tex> \left[ \begin{array}{ccc} x_1 \\ x_2 \\\end{array} \right]</tex> <tex> \left[ \begin{array}{ccc} x_1 \\ x_2 \\\end{array} \right]</tex>](lib/plugins/latex/images/d6ca1870cf7624fc9f8143ed876b4ff99773f377_0.png)
Por lo tanto ![<tex>P = \left[ \begin{array}{ccc} 1 & 0 \\ 0 & 2 \\\end{array} \right]</tex> <tex>P = \left[ \begin{array}{ccc} 1 & 0 \\ 0 & 2 \\\end{array} \right]</tex>](lib/plugins/latex/images/a7beeb9550975e3e10e627561c2f2fcf1cd14f39_0.png)
Ahora voy a analizar la ecuación 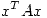
Obtengo: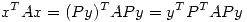 con
con
![<tex>A = \left[ \begin{array}{ccc} 4 & 2 \\ 2 & 1 \\\end{array} \right]</tex> <tex>A = \left[ \begin{array}{ccc} 4 & 2 \\ 2 & 1 \\\end{array} \right]</tex>](lib/plugins/latex/images/a73a75111d84da78e9d2771d3f8c82e340a7d521_0.png)
Busco el máximo de![<tex>y^T P^T A P y = y^T \left[ \begin{array}{ccc} 4 & 4 \\ 4 & 4 \\\end{array} \right] y</tex> <tex>y^T P^T A P y = y^T \left[ \begin{array}{ccc} 4 & 4 \\ 4 & 4 \\\end{array} \right] y</tex>](lib/plugins/latex/images/a03698224ac1f86eda04bba87c0c569b55567653_0.png)
A simple viste se puede observar que 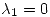 y
y 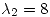
Por lo tanto en 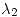 va a estar el máximo
va a estar el máximo
![<tex> S_\lambda = Nu(P^T A P - \lambda I)= Nu(\left[ \begin{array}{ccc} -4 & 4 \\ 4 & -4 \\\end{array} \right]) </tex> <tex> S_\lambda = Nu(P^T A P - \lambda I)= Nu(\left[ \begin{array}{ccc} -4 & 4 \\ 4 & -4 \\\end{array} \right]) </tex>](lib/plugins/latex/images/a922a28010f8d973ac3757a7ae04419153394e30_0.png)
![<tex> S_\lambda = gen{[1 \quad 1]^T}</tex> <tex> S_\lambda = gen{[1 \quad 1]^T}</tex>](lib/plugins/latex/images/734626c37488d17b72269d468358746b416140f7_0.png) / como tenia que ser de norma 1
/ como tenia que ser de norma 1 ![<tex>y=\pm [1/\sqrt 2 \quad 1/\sqrt 2]^T</tex> <tex>y=\pm [1/\sqrt 2 \quad 1/\sqrt 2]^T</tex>](lib/plugins/latex/images/f6e6cc30a4424cd93a6c610f7847b8a47f9e030f_0.png)
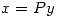 /
/ ![<tex>x=\left[ \begin{array}{ccc} 1 & 0 \\ 0 & 2 \\\end{array} \right]\left[ \begin{array}{ccc} 1/\sqrt 2 \\1/\sqrt 2 \\\end{array} \right]</tex> <tex>x=\left[ \begin{array}{ccc} 1 & 0 \\ 0 & 2 \\\end{array} \right]\left[ \begin{array}{ccc} 1/\sqrt 2 \\1/\sqrt 2 \\\end{array} \right]</tex>](lib/plugins/latex/images/3e043d866484f8fc018dfba317d54a098d682aba_0.png)
![<tex>x = \left[ \begin{array}{ccc} 1/\sqrt 2 \\2/\sqrt 2 \\\end{array} \right]</tex> <tex>x = \left[ \begin{array}{ccc} 1/\sqrt 2 \\2/\sqrt 2 \\\end{array} \right]</tex>](lib/plugins/latex/images/17da912cd1da49ea6249363b9b43e65dc2c32d16_0.png)
El máximo va a estar en ![<tex>x = \pm [1/\sqrt 2 \quad 2/\sqrt 2]^T</tex> <tex>x = \pm [1/\sqrt 2 \quad 2/\sqrt 2]^T</tex>](lib/plugins/latex/images/a3c4a6f4bb6e2007af381cc4eb974bf21090275b_0.png)
Resolución Ejercicio 3)
Resolución Ejercicio 4)
(a)
Primero voy a escribir a  como
como 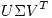 como
como 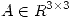 entonces
entonces
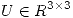
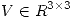
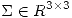
![<tex>V = \left[ \begin{array}{ccc} a & d & 0 \\ b & e & 1/\sqrt 2 \\c & f & -1/\sqrt 2 \end{array} \right]</tex> <tex>V = \left[ \begin{array}{ccc} a & d & 0 \\ b & e & 1/\sqrt 2 \\c & f & -1/\sqrt 2 \end{array} \right]</tex>](lib/plugins/latex/images/a721db3bd577a3172c3fc2517881baed028b292d_0.png)
![<tex>U = \left[ \begin{array}{ccc} o & r & -1/\sqrt 2 \\ p & s & 0 \\q & t & 1/\sqrt 2 \end{array} \right]</tex> <tex>U = \left[ \begin{array}{ccc} o & r & -1/\sqrt 2 \\ p & s & 0 \\q & t & 1/\sqrt 2 \end{array} \right]</tex>](lib/plugins/latex/images/3e95c3b697089c5fddc64362de01dfc6ca4d5df0_0.png)
![<tex>\Sigma = \left[ \begin{array}{ccc} 3 & 0 & 01 \\ 0 & 2 & 0 \\0 & 0 & 0 \end{array} \right]</tex> <tex>\Sigma = \left[ \begin{array}{ccc} 3 & 0 & 01 \\ 0 & 2 & 0 \\0 & 0 & 0 \end{array} \right]</tex>](lib/plugins/latex/images/cbf57569b0b11bb4fe38f869e798fe6c27f53087_0.png)
tal que la 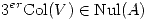 y la
y la 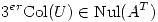 , siendo
, siendo 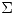 las raices de los autovalores de
las raices de los autovalores de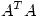
Entonces lo que hay que hacer es completar esas dos matrices con valores tal que  y
y 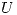 sean matrices ortogonales, no son valores muy dificiles de sacar, por lo tanto pongo directamente
sean matrices ortogonales, no son valores muy dificiles de sacar, por lo tanto pongo directamente
![<tex>V = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1/\sqrt 2& 1/\sqrt 2 \\0 & 1/\sqrt 2 & -1/\sqrt 2 \end{array} \right]</tex> <tex>V = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1/\sqrt 2& 1/\sqrt 2 \\0 & 1/\sqrt 2 & -1/\sqrt 2 \end{array} \right]</tex>](lib/plugins/latex/images/d207fb2e711e7d9f7144143e16782fdcb7306f4f_0.png)
![<tex>U = \left[ \begin{array}{ccc} -1/\sqrt 2 & 0 & -1/\sqrt 2 \\ 0 & 1 & 0 \\-1/\sqrt 2 & 0 & 1/\sqrt 2 \end{array} \right]</tex> <tex>U = \left[ \begin{array}{ccc} -1/\sqrt 2 & 0 & -1/\sqrt 2 \\ 0 & 1 & 0 \\-1/\sqrt 2 & 0 & 1/\sqrt 2 \end{array} \right]</tex>](lib/plugins/latex/images/84085d7890527e0bc41d3d182e5bdd826fa845fc_0.png)
 es simétrica, por lo tanto puedo decir que
es simétrica, por lo tanto puedo decir que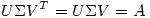
Calculando: ![<tex>A=\left[ \begin{array}{ccc} (-3\sqrt 2)/2 & 0 & 0 \\ 0 & \sqrt 2& 0 \\(-3\sqrt 2)/2 & 0 & \sqrt 2 \end{array} \right]</tex> <tex>A=\left[ \begin{array}{ccc} (-3\sqrt 2)/2 & 0 & 0 \\ 0 & \sqrt 2& 0 \\(-3\sqrt 2)/2 & 0 & \sqrt 2 \end{array} \right]</tex>](lib/plugins/latex/images/222a9c703457374cb19b94efa2e4b3c00b7b6095_0.png)
