Coloquio 21/12/2005
Enunciado
1) Sea  y sea
y sea 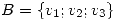 una base de
una base de  . (a) Sabiendo que para cierta base
. (a) Sabiendo que para cierta base 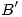 de
de  ,
,
![<tex>[T]_{B'} = \left[ \begin{array}{ccc} \alpha + 1 & 1 & 0 \\ 0 & 1 & 0 \\0 & 0 & -1 \end{array} \right]</tex> <tex>[T]_{B'} = \left[ \begin{array}{ccc} \alpha + 1 & 1 & 0 \\ 0 & 1 & 0 \\0 & 0 & -1 \end{array} \right]</tex>](lib/plugins/latex/images/37a1fdc291527e00e169b14c47ce3c2644ecf037_0.png) , determine los valores de
, determine los valores de 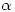 . para los cuales
. para los cuales ![<tex>[T]_B</tex> <tex>[T]_B</tex>](lib/plugins/latex/images/77974c5d33422dda29ab8c19452e9cbe246a3fa1_0.png) es diagonalizable.
es diagonalizable.
(b) Considerando 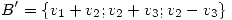 y
y 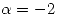 , hallar los autovalores y autoespacios de
, hallar los autovalores y autoespacios de 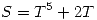 .
.
2) (a) Sea 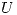 ortogonal y tal que
ortogonal y tal que 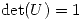 . Probar que existe
. Probar que existe 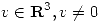 , tal que
, tal que 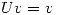 .
(b) Probar que si
.
(b) Probar que si 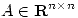 es simétrica y tal que
es simétrica y tal que 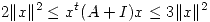 para todo
para todo 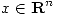 , entonces
, entonces  es inversible y los autovalores de
es inversible y los autovalores de 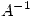 pertenecen al intervalo
pertenecen al intervalo ![<tex>[0.5,\;1]</tex> <tex>[0.5,\;1]</tex>](lib/plugins/latex/images/34c5772f094c339f4d9eae1efc417040267d1507_0.png)
3) La temperatura del punto ![<tex> [x_1 \quad x_2]^t </tex> <tex> [x_1 \quad x_2]^t </tex>](lib/plugins/latex/images/b6609ab918cb92fbe691b025e2ce8a5370a46848_0.png) del plano es
del plano es 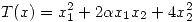
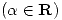 .
(a)Hallar los valores de
.
(a)Hallar los valores de 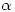 para los cuales las isotermas son curvas cerradas.
(b) Considerando
para los cuales las isotermas son curvas cerradas.
(b) Considerando  , hallar los puntos de la curva
, hallar los puntos de la curva 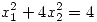 en los cuales la temperatura es mínima.
en los cuales la temperatura es mínima.
4) (a) Hallar 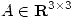 tal que 4 y 1 sean autovalores de
tal que 4 y 1 sean autovalores de 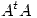 ,
, ![<tex> [1 \quad 1 \quad 0]^t \in \mathrm{Nul} (A) </tex> <tex> [1 \quad 1 \quad 0]^t \in \mathrm{Nul} (A) </tex>](lib/plugins/latex/images/709617d1510456aca2c1f2b25642251ffd203816_0.png) y
y ![<tex> [1 \quad 0 \quad 1]^t \in \mathrm{Nul} (A^t)</tex> <tex> [1 \quad 0 \quad 1]^t \in \mathrm{Nul} (A^t)</tex>](lib/plugins/latex/images/5fd751d0e5b9aa6d4030fa386bfea902ac5ffe56_0.png) .
.
(b) Sabiendo que 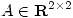 es simétrica y tal que
es simétrica y tal que ![<tex>A[1\quad 2]^t = [2 \quad 4]^t </tex> <tex>A[1\quad 2]^t = [2 \quad 4]^t </tex>](lib/plugins/latex/images/d6a0d839b3df0b0ad40e37992292b15a268105fd_0.png) y
y 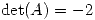 , hallar la solución del problema a valor inicial
, hallar la solución del problema a valor inicial 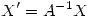 ,
, ![<tex>X(0) = [1 \quad 0 ]^t</tex> <tex>X(0) = [1 \quad 0 ]^t</tex>](lib/plugins/latex/images/0e6603c6a08a471a105f55d9db211a0bca67a4bf_0.png) .
.
Los alumnos del 2do cuatrimestre de 2004 o del 1ro de 2005 deben reemplazar el punto 4(b) por el siguiente:
(b*) Sea 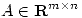 . Probar que
. Probar que 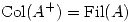 y que
y que 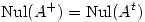 .
.
El examen se aprueba resolviendo correctamente al menos cuatro puntos. Justifique todas sus rerspuestas.
Resolución Ejercicio 1)
1.a)
 es diagonalizable sii las multiplicidades algebráica y geómetrica de todos sus autovalores coinciden. Empezamos obteniendo los autovalores de
es diagonalizable sii las multiplicidades algebráica y geómetrica de todos sus autovalores coinciden. Empezamos obteniendo los autovalores de ![<tex>[T]_B</tex> <tex>[T]_B</tex>](lib/plugins/latex/images/77974c5d33422dda29ab8c19452e9cbe246a3fa1_0.png) .
.
![<tex>[T_B] - \lambda I = \left( \begin{array}{ccc} \alpha+1-\lambda & 1 & 0 \\ 0 & 1 - \lambda & 0 \\ 0 & 0 & -1-\lambda \end{array} \right) </tex> <tex>[T_B] - \lambda I = \left( \begin{array}{ccc} \alpha+1-\lambda & 1 & 0 \\ 0 & 1 - \lambda & 0 \\ 0 & 0 & -1-\lambda \end{array} \right) </tex>](lib/plugins/latex/images/4b8ad03e87e44a7625cf34a2630681749cec1cb1_0.png)
![<tex>p(\lambda) = det( [T_B] - \lambda I) = -(1+\lambda)(1-\lambda)(\alpha+1-\lambda) = 0 </tex> <tex>p(\lambda) = det( [T_B] - \lambda I) = -(1+\lambda)(1-\lambda)(\alpha+1-\lambda) = 0 </tex>](lib/plugins/latex/images/9a7259527029cf855ac4b386cfd6a3e9b3cbffa8_0.png)
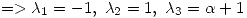
Si los tres autovalores son distintos, entonces sus multiplicidades algebráicas y geométricas son 1. Por lo tanto para 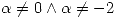 se verifica que
se verifica que  es diagonalizable. Ahora vamos a los dos casos más puntuales:
es diagonalizable. Ahora vamos a los dos casos más puntuales:
Con  ,
, 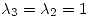
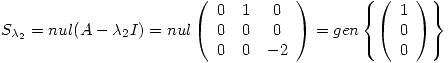
Como para 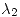 la multiplicidad algebráica
la multiplicidad algebráica 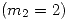 es diferente de la geométrica
es diferente de la geométrica 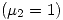 , entonces con
, entonces con  ,
,  no es diagobalizable.
no es diagobalizable.
Con 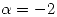 ,
, 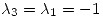
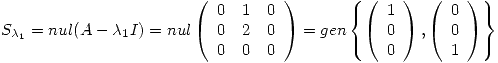
Como para 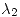 la multiplicidad algebráica
la multiplicidad algebráica 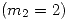 es igual a la geométrica
es igual a la geométrica 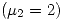 , entonces con
, entonces con 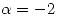 ,
,  es diagobalizable.
es diagobalizable.
Así podemos recopilar todo y decir que  es diagonalizable
es diagonalizable 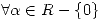
1.b)
Para este insciso del ejercicio vamos a usar dos resultados del ejercicio anterior:
[list]- Si 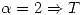 es diagonalizable y
es diagonalizable y 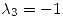 -
- ![<tex>[T_{B'}] = P D_T P^{-1}</tex> <tex>[T_{B'}] = P D_T P^{-1}</tex>](lib/plugins/latex/images/41bdcf61478530161f8c159a8ecd208f1b107694_0.png) siendo
siendo  y
y  una matriz cuyas columnas son una base de
una matriz cuyas columnas son una base de 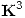 formada por autovectores de
formada por autovectores de ![<tex>[T_{B'}]</tex> <tex>[T_{B'}]</tex>](lib/plugins/latex/images/b16cf5835585e28cd08dd9c30bd6d5b7c7062c6e_0.png) ordenados de la misma manera que sus autovalores asociados lo están en
ordenados de la misma manera que sus autovalores asociados lo están en 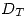 [/list]
Entonces comenzamos a resolver el ejercicio:
[/list]
Entonces comenzamos a resolver el ejercicio:
![<tex>[S_{B'}]=[T_{B'}]^5 + 2 [T_{B'}] = P {D_T}^5 P^{-1} + 2 ( P D_T P^{-1}) = P ( {D_T}^5 + 2 D_T ) P^{-1}</tex> <tex>[S_{B'}]=[T_{B'}]^5 + 2 [T_{B'}] = P {D_T}^5 P^{-1} + 2 ( P D_T P^{-1}) = P ( {D_T}^5 + 2 D_T ) P^{-1}</tex>](lib/plugins/latex/images/230022aec75a025d4694c3bfbbc0a7c6b1434b08_0.png)
La primera igualdad se da por ser ![<tex>[T_{B'}]</tex> <tex>[T_{B'}]</tex>](lib/plugins/latex/images/b16cf5835585e28cd08dd9c30bd6d5b7c7062c6e_0.png) diagonalizable. En la segunda simplemente agrupamos. Por último podemos reemplazar de la siguiente manera:
diagonalizable. En la segunda simplemente agrupamos. Por último podemos reemplazar de la siguiente manera:
![<tex>[S_{B'}] = P D_S P^{-1}</tex> <tex>[S_{B'}] = P D_S P^{-1}</tex>](lib/plugins/latex/images/f817c607c588395316ee80346d5778b91d69e87a_0.png) con
con 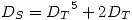
De aquí sacamos que:
[list]- Los autoespacios de  son los mismos que los de
son los mismos que los de  .
- Un autovalor
.
- Un autovalor 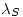 de
de  es
es 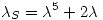 siendo
siendo  un autovalor de
un autovalor de  .[/list]
Luego los autovalores de
.[/list]
Luego los autovalores de  son
son 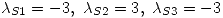 y los autoespacios asociados son:
y los autoespacios asociados son: