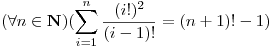Examen (Parcial) - 61.07. Matemática Discreta
Cátedra: Todas
Fecha: 1er Oportunidad - (1er Cuatrimestre) 2009
Día: 16/05/2009
Enunciado
1 Sea  la relación definida en
la relación definida en 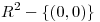 por
por 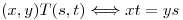 .
.
a) Probar que  es una relación de equivalencia.
es una relación de equivalencia.
b) Caracterizar geométricamente las clases de  .
.
c) Si la anterior relación se define en 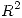 , ¿es una relación de equivalencia? ¿Por qué?
, ¿es una relación de equivalencia? ¿Por qué?
2 Sea 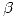 un álgebra de Boole con exactamente
un álgebra de Boole con exactamente  átomos que son
átomos que son 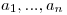 .
.
a) ¿Cuántas soluciones tiene el siguiente sistema?
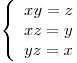
b) Si 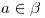 es tal que:
es tal que: 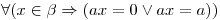 , entonces
, entonces 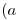 es un átomo
es un átomo 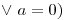 .
.
c) Probar:  .
.
3 Teniendo en cuenta que todo punto de 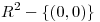 se escribe en forma única:
se escribe en forma única:
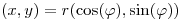 con
con  y
y 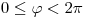 , se define la siguiente relación en
, se define la siguiente relación en 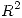 :
:
Si 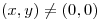 ,
, 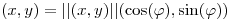 y si
y si 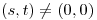 ,
, 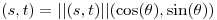 :
:
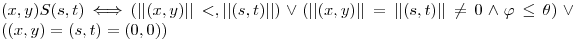
a) Probar que  es una relación de orden.
es una relación de orden.
b) Probar que es un orden total.
c) ¿Existe un mínimo de 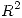 ?
?
4 Sea  con
con 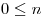 una relación de recurrencia de segundo orden con coeficientes constantes .
una relación de recurrencia de segundo orden con coeficientes constantes .
Sabiendo que 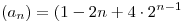 y
y 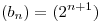 son soluciones de la ecuación dada, determine
son soluciones de la ecuación dada, determine 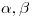 y
y 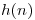 .
.
5
a) Sean 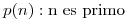 y
y  definidas en
definidas en  .
.
Determinar cuales de las siguientes proposiciones son verdaderas o falsas. Justificar la respuesta.
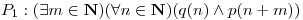
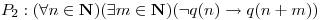
b)