Examen (Parcial) - 61.07. Matemática Discreta
Cátedra: todas
Fecha: 1er Oportunidad - (2do Cuatrimestre) 2008
Día: 25/10/2008
Enunciado
1 Se define en 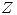 la siguiente relación:
la siguiente relación:
![<tex>aRb \leftrightarrow \ [(a\geq b\ \wedge \ a-b \ es \ par) \vee \ ( a \ es \ par \wedge \ b\ es\ impar)]</tex> <tex>aRb \leftrightarrow \ [(a\geq b\ \wedge \ a-b \ es \ par) \vee \ ( a \ es \ par \wedge \ b\ es\ impar)]</tex>](lib/plugins/latex/images/0022d283e592b68f9c8953a163f7a102ba2f6552_0.png)
a) Probar que es un orden total.
b) Confeccionar el diagrama de Hasse para R restringida a 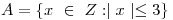 .
.
c) ¿Existe algún subconjunto de 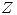 que tiene ínfimo pero no mínimo? Justifíque.
d) ¿Existe algún subconjunto infinito de
que tiene ínfimo pero no mínimo? Justifíque.
d) ¿Existe algún subconjunto infinito de 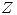 que tiene ínfimo y supremo? Justifíque.
que tiene ínfimo y supremo? Justifíque.
2 En 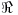 se define la siguiente relación:
se define la siguiente relación:
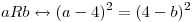
a) Probar que es una relación de equivalencia.
b) Hallar el conjunto cociente.
3 Determinar el valor de verdad de las siguientes proposiciones (JUSTIFIQUE):
a) 
b) 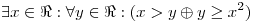
4
a) Resuelva la siguiente ecuación de recurrencia:
 con
con 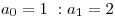
b) Demuestre utilizando el principio de inducción:
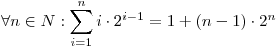
5 En una materia de la facultad los docentes han confeccionado un examen que consta de 5 ejercicios: A,B,C,D, y E. Para aprobar el examen exiten ciertos requisitos:
- Si el ejercicio A está mal resuelto, NO se aprueba, independientemente de como estén los demás.
- Si el ejercicio B no está bien resuelto entonces sí o sí deben estarlo el C y el E para poder aprobar.
- Si los ejercicios D y E están ambos incorrectos tampoco se aprueba.
Salvo estas tres condiciones en el resto de los casos se aprueba. Se pide:
a) Arme la tabla de la función booleana de variables A,B,C,D, y E, cuyo resultado sea 1 si se aprueba el examen y 0 si no lo aprueba.
b) ¿Es suficiente para poder aprobar tener 3 ejercicios correctos? ¿Y 4 correctos? Justifíque.
c) ¿Es necesario para aprobar tener 3 ejercicios correctos? ¿Y 4 correctos? Justifíque.
d) Escriba la función booleana en forma normal disyuntiva, simplifique la expresión de la función booleana a su mínima expresión y construya un circuito que sólo tenga compuertas NOR.
