1. Sea la ecuación de recurrencia ;
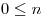
   1. a)Sabiendo que (2ⁿ + 1) es solución de la ecuación homogenea asociada a la dada, hallar los coeficientes α y β pertenecientes a los reales y resolver dicha ecuación homogénea.
   2. b) Encontrar la solución de la ecuación dada que satisface
      
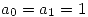
2. 1. a) Sea B un álgebra de Boole, probar que para todo par de elementos x, y pertenecientes a B se cumple:
      sup {x, y} = x + y ínf {x, y} = x.y
   2. b) Sea la función booleana f: {0,1}⁴ –> {0,1} que solo vale 1 en las cuaternas que no tienen dos 0 consecutivos.
      1. i) Encontrar su expresión como suma de miniterminos.
      2. ii) Encontrar una expresion simplificada, y luego con un circuito de compuertas NAND
3. Se define en R2 la siguiente relación
   (x,y)T(z,w) ⇐⇒ x.y = z.w
   1. a) Probar que es una relación de equialencia.
   2. b) Calcular y graficar la clase de equivalencia correspondiente a (π, e).
   3. c) Hallar la partición que genera.
4. Se define en R2 la siguiente relación:
   (x,y)S(z,w) ⇐⇒ (x� �z) y (y≥w)
   1. a) Probar que es una relación de orden en R2. ¿Es total?.
   2. b) Determinar todos los elementos particualares de los siguientes conjuntos:
      A = {(0,0); (0,1); (2,1); (1,2)}
      B = {(x,y) : |x| + |y| = 2}
      
5. 1. a) Dos países han entrado en colisión. El ministro de Defensa de uno de los países le propone a su presidente tres estrategias de defensa de modo que:
      Si la estrategia I se lleva a cabo, la estrategia II no se lleva a cabo.
      Si la estrategia I no se lleva a cabo, la estrategia III se lleva a cabo.
      Si la estragia II se lleva a cabo, la estrategia III no se lleva a cabo.\\¿Se puede saber, por medio de alguna derivación lógica, si alguna de las estrategias de llevó o no a cabo.
   2. b) Probar utiliando el principio de inducción:

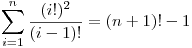
Justifique todos los pasos realizados

Para la realización del parcial dieron 2 horas y media.