Tabla de Contenidos
Examen Final - 61.07. Matemática Discreta - 17/07/2013
Cátedra: Todas
Día: 17/07/2013
Enunciado
Resolución
Ejercicio 5
b)
Se tiene un grafo disconexo de 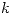 componentes (subgrafos conexos) y
componentes (subgrafos conexos) y  vértices. La cantidad de aristas se maximiza cuando todas excepto una (k - 1) de las componentes del grafo son vértices aislados (si una de estas componentes tuviese dos vértices, uno de ellos se puede llevar a otra componente con más vértices y generaría más aristas entre estos últimos vértices). La última componente, claramente, sería un grafo K-regular.
vértices. La cantidad de aristas se maximiza cuando todas excepto una (k - 1) de las componentes del grafo son vértices aislados (si una de estas componentes tuviese dos vértices, uno de ellos se puede llevar a otra componente con más vértices y generaría más aristas entre estos últimos vértices). La última componente, claramente, sería un grafo K-regular.
Entonces se tienen  vértices aislados y un grafo
vértices aislados y un grafo 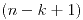 -regular. Ahora bien, para un grafo genérico k-regular la cantidad de aristas está determinada por
-regular. Ahora bien, para un grafo genérico k-regular la cantidad de aristas está determinada por
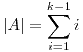
Y para el caso, se tiene que
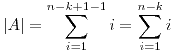
A esta sumatoria le aplicamos Gauss para que finalmente nos quede expresada como
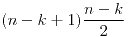 ■
■
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported



