Tabla de Contenidos
Examen Final - 61.07. Matemática Discreta - 26 de Diciembre de 2007
Cátedra: Cátedra 03
Fecha: Oportunidad X - Verano 2007
Día: 26/12/2007
Esta página está incompleta; podés ayudar completando el material.
Enunciado
Punto I
- Definir álgebra de Boole y dar un ejemplo con más de cinco elementos.
- Definir átomo en un álgebra de Boole y mostrar cuáles lo son en el ejemplo dado en la parte a).
- Probar que un álgebra de Boole tiene exactamente
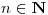 átomos si y sólo si posee
átomos si y sólo si posee 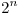 .
.
Punto II
- Definir relación de equivalencia en un conjunto.
- Definir relación de orden en un conjunto.
- Probar que
 es una relación de equivalencia y de orden en un conjunto
es una relación de equivalencia y de orden en un conjunto  si y sólo si
si y sólo si 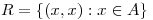 .
.
Punto III
- Definir árbol generador de un grafo y probar que un grafo posee un árbol generador si y sólo si es conexo.
- Sea
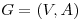 un grafo conexo y
un grafo conexo y  tal que ningún ciclo o circuito de
tal que ningún ciclo o circuito de 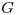 tiene todas sus aristas pertenecientes a
tiene todas sus aristas pertenecientes a 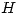 . Probar que existe un árbol generador de
. Probar que existe un árbol generador de 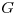 que posee todas las aristas de
que posee todas las aristas de 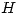 .
.
Punto IV
- Dar la definición de árbol y demostrar una propiedad equivalente a ella.
- Probar que si un árbol posee un vértice de grado
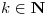 entonces posee por lo menos
entonces posee por lo menos 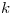 vértices de grado
vértices de grado  .
.
Punto V
- Definir red de transporte y dar un ejemplo con por lo menos
 vértices.
vértices. - Definir flujo y su valor. Dar un ejemplo en la red dada en a).
- Definir corte y su capacidad. Dar un ejemplo de la red dada en a).
- Probar que si
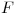 es un flujo y
es un flujo y 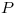 es un corte en la misma red, entonces
es un corte en la misma red, entonces 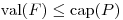
Justifique todos los pasos realizados.
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
