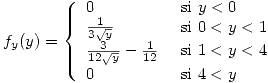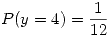Examen Parcial - 61.06. Probabilidad y Estadística A - Industrial
Cátedra: García Argiz
Fecha: 2ºCuatrimestre 1º Oportunidad - 2002
Día: 23/10/2002
Enunciado
Punto I
Se tienen una partida (tipo A) de 15 artículos dos de los cuales son defectuosos y dos partidas (tipo B) con 20 artículos en c/u y con tres defectuosos en cada una de ellas. Se eligen dos partidas al azar y se extraen sucesivamente y simultáneamente los artículos de c/u de ellas hasta encontrar el primero defectuoso en alguna de las dos. Se sabe que se efectuó exactamente una extracción en cada partida, ¿Cuál es la probabilidad de haber elegido las dos tipo B?
Punto II
Sea la función de densidad
 .
.
Hallar la función de densidad 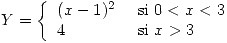
Punto III
Los repuestos que se reciben en un comercio pertenecen a dos proveedores; el 60% se reciben de A y el resto de B. La duración de los repuestos es aleatoria en horas con funciones de densidad respectivamente:
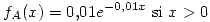

Se descartan los repuestos que duran menos de 85 hs.
Calcular la probabilidad de que en 8 repuestos elegidos al azar a lo sumo 3 duren más de 105 horas si se sabe que no han sido descartados.
Punto IV
Un robot industrial fabrica una determinada parte de una pieza. Hay una probabilidad del 5% que la fabrique defectuosa. Se controla la producción revisando una muestra de “n” partes con un control automático que trabaja con una confiabilidad del 90% para las defectuosas y del 95% para las buenas.
Si el control determina que hay por lo menos una pieza defectuosa se revisa el proceso de fabricación.
Calcular el tamaño de la muestra para que la probabilidad de revisar el proceso sea del 92%.
Punto V
Se tienen dos cajas con 9 bolitas verdes y 1 roja la 1º y con 10 verdes y 5 rojas la 2º caja.
Se tira una vez un dado común equilibrado, si sale 1, 2 o 3 se elige la caja 1; si sale 4 o 5 la caja 2 y si sale 6 se elige con igual probabilidad cualquiera de las dos cajas.
Se extraen al azar una bolita de la caja elegida y dos de la otra caja y se colocan en una tercera caja.
Calcular la función de probabilidad de la cantidad de bolitas rojas en la 3º caja.
Resolución
Punto I
| Partidas | |
|---|---|
| A | B |
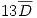 | 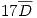 |
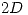 |  |


x: Número de artículos defectuosos al extraer sucesiva y simultáneamente un artículo de dos partidas.
Para la primera extracción tenemos las siguientes dos tablas…
| Caso Partidas AB | Caso Partidas BB | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| x | A | x | B | |||||||
| 0 | 1 | 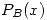 | 0 | 1 | 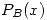 |
|||||
| 0 | 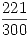 | 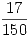 | 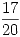 | 0 | 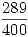 |  | 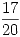 |
|||
| B | 1 |  |  |  | B | 1 |  | 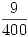 |  |
|
 |  |  | 1 | 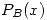 |  |  | 1 | |||
La probabilidad de obtener al menos un artículo defectuoso en la primer extracción es:
![<tex>P(x>0) = P \left[ (A \cap B ) \cap P \left( \frac{x>0}{A\cap B} \right) \right] \cup P \left[ (B\cap B) \cap P \left( \frac{x>0}{B\cap B} \right) \right] = \\ = \frac{2}{3}\times \left[ 1- P \left( \frac{x=0}{A\cap B}\right)\right] + \frac{1}{3}\times \left[ 1 - P\left( \frac{x=0}{B\cap B}\right)\right] = \\ = \frac{2}{3}\times\frac{79}{300} + \frac{1}{3}\times\frac{111}{400} = \frac{79}{450} + \frac{37}{400} = \frac{193}{720} = 0.2681 </tex> <tex>P(x>0) = P \left[ (A \cap B ) \cap P \left( \frac{x>0}{A\cap B} \right) \right] \cup P \left[ (B\cap B) \cap P \left( \frac{x>0}{B\cap B} \right) \right] = \\ = \frac{2}{3}\times \left[ 1- P \left( \frac{x=0}{A\cap B}\right)\right] + \frac{1}{3}\times \left[ 1 - P\left( \frac{x=0}{B\cap B}\right)\right] = \\ = \frac{2}{3}\times\frac{79}{300} + \frac{1}{3}\times\frac{111}{400} = \frac{79}{450} + \frac{37}{400} = \frac{193}{720} = 0.2681 </tex>](lib/plugins/latex/images/872ea38aaeb8e0d2fd7fa09f757f1ff7750b6315_0.png)
Yo sé que encontré al menos un artículo defectuoso en la primera extracción (la probabilidad de tal evento es  ) con ésta información me interesa saber la probabilidad de haber elegido las dos partidas tipo B.
) con ésta información me interesa saber la probabilidad de haber elegido las dos partidas tipo B.
Dicha probabilidad será, entonces:
 —-
—-
Punto II
Punto III
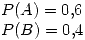
 Probabilidad de que el repuesto provenga de la fábrica A o B
Probabilidad de que el repuesto provenga de la fábrica A o B
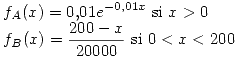
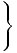 Funciones de densidad de la duración de los repuestos.
Funciones de densidad de la duración de los repuestos.
x: duración del repuesto, en hs
D: evento tal que un repuesto sea descartado, dure menos de 85 hs.


Hasta acá tenemos:

Entonces:
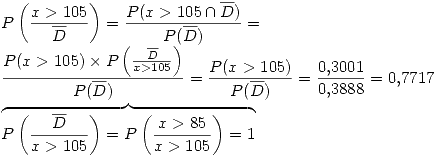
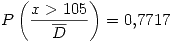
y: cantidad de repuestos que duran mas de 105 horas entre 8 repuestos que no han sido descartados.
Puedo decir que es un proceso de Bernoulli:
- Consiste en n repeticiones de revisar si dura mas de 105 horas
- Se pueden clasificar los resultados como éxito (x>105) o fracaso (x<105hs)
- La probabilidad de éxito (
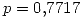 ) permanece constante
) permanece constante
- Cada revisión es independiente
Entonces 
Sea C: evento tal que en 8 repuestos, que sé que no han sido descartados, encuentre a lo sumo 3 que duren más de 105
horas (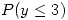 )
)

![<tex>P(C)=P\left( y \leq 3\right)= P(y=3) + P(y=2) + P(y=1) + P(y=0) = \\ = {8 \choose 3}\times(0.7717)^3\times(0.2283)^5 +{8 \choose 2}\times(0.7717)^2\times(0.2283)^6 + \\ +{8 \choose 1}\times(0.7717)\times(0.2283)^7 +{8 \choose 0}\times(0.2283)^8 = \\= (0.2283)^5\times\left[56\times0.7717^3+28\times0.7717^2\times0.2283+8\times0.7717\times0.2283^2+0.2283^3\right] = \\ = 0.2283^5\times\left[25.7355+3.8068+0.3217+0.01189\right] = 0.01853 </tex> <tex>P(C)=P\left( y \leq 3\right)= P(y=3) + P(y=2) + P(y=1) + P(y=0) = \\ = {8 \choose 3}\times(0.7717)^3\times(0.2283)^5 +{8 \choose 2}\times(0.7717)^2\times(0.2283)^6 + \\ +{8 \choose 1}\times(0.7717)\times(0.2283)^7 +{8 \choose 0}\times(0.2283)^8 = \\= (0.2283)^5\times\left[56\times0.7717^3+28\times0.7717^2\times0.2283+8\times0.7717\times0.2283^2+0.2283^3\right] = \\ = 0.2283^5\times\left[25.7355+3.8068+0.3217+0.01189\right] = 0.01853 </tex>](lib/plugins/latex/images/409936ea9bde59f8c4475461e6097ea7e7ee30dc_0.png)
Punto IV
 tengo que hacer el arbol….
tengo que hacer el arbol….
D: La pieza es defectuosa
R: Evento tal que el proceso encuentre una pieza defectuosa

x:cantidad de piezas con la característica R en una muestra de n piezas

Si al menos una pieza tiene la característica R, se revisa el proceso, esto es, si 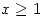
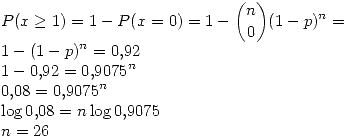
Discusión
TO DO
Ejercicio 1— Claus 2006/06/01 01:16Ejercicio 2Listo, gracias Cornell y fhran! por las manos — Claus 2006/06/07 10:46Ejercicio 3— Claus 2006/06/03 18:45Ejercicio 4Falta el arbol — Claus 2006/06/04 13:41- Ejercicio 5

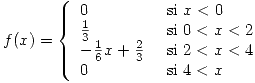



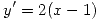
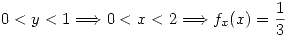


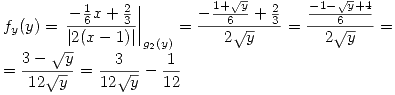

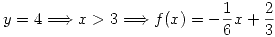 , tengo un punto pesado,
, tengo un punto pesado, ![<tex>P(y=4)= \int_3^4 f(x)\, dx = -\frac{1}{6}\int_3^4 x\, dx +\frac{2}{3}\int_3^4 \, dx = \\= -\frac{1}{6}\left[\frac{16-9}{2}\right]+\frac{2}{3}\left[4-3\right] = -\frac{7}{12}+\frac{2}{3}=\frac{1}{12}</tex> <tex>P(y=4)= \int_3^4 f(x)\, dx = -\frac{1}{6}\int_3^4 x\, dx +\frac{2}{3}\int_3^4 \, dx = \\= -\frac{1}{6}\left[\frac{16-9}{2}\right]+\frac{2}{3}\left[4-3\right] = -\frac{7}{12}+\frac{2}{3}=\frac{1}{12}</tex>](lib/plugins/latex/images/f85194427801ad7b0d800c1d21bda51fea825fd9_0.png)