Examen Parcial (1) - 61.06 Probabilidad y Estadística (no industrial) - 21/05/2011
Cátedra: Sacerdoti / Baliña / Kornblit
Fecha: 1º Parcial - 1º Oportunidad - 1º Cuatrimestre 2011
Día: 21/05/2011
Tema: 2
Enunciado
Punto 1
Un granjero sabe que el peso P0 de sus pollitos al nacer es U(200 g; 280g), y que la distribución del peso P1 de un pollo adulto, condicional a P0, es U(12 P0; 15 P0)
| a) | Hallar la probabilidad de que un pollo adulto de 3,6 kg haya pesado al nacer más de 270 g. |
| b) | Hallar la función de regresión de P1 dado P0 y la covarianza entre ambas variables. |
Punto 2
Otro granjero, en cambio, sabe que el peso de sus pollos adultos en N(3,2 kg, 0,2 kg), que el costo fijo de crianza se estima en $20 por animal, y que el precio de venta es el siguiente:
- los pollos que pesan más de 3,4 kg se venden a $10 por kilo,
- los novillos que pesan menos de 3,4 kg se venden a $8 por kilo,
- el tope en todos los casos es de $36 por animal.
| a) | Hallar la probabilidad de ganar más de $12 netos al vender un pollo seleccionado al azar. |
| b) | Hallar la media de la ganancia neta. |
Punto 3
En una empresa se produce harina de trigo en dos molinos, que trabajan independientemente. La producción diaria en cada molino (en toneladas) tiene función de densidad:
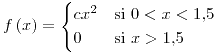
| a) | Hallar la probabilidad de que en un día ambos molinos totalicen total más de 2,5 t. |
| b) | Hallar la probabilidad de que, en una semana, haya al menos un día en el que el molino que menos trabaja produzca más de 1 t. |
Punto 4
Para la aceptación de un lote de discos de freno, se realiza el siguiente control de calidad: Se toma una muestra de 30 unidades, y se la somete a un ensayo de durabilidad. Si los 30 responden satisfactoriamente, se acepta el lote, si dos o más discos no responden, se lo rechaza. Si sólo un disco es defectuoso, se toma otra muestra de 15 unidades, aceptando el lote sólo si en la segunda muestra todos los discos pasan satisfactoriamente el ensayo.
| a) | Calcular la función de probabilidad del número total de discos defectuosos encontrados en los ensayos, si la proporción de defectuosos es p = 0,03 (Nota: es valido aproximar por 0 las probabilidades que, a su criterio, sean muy pequeñas). |
| b) | Calcular la probabilidad de aceptar el lote para varios valores de p, y trazar un gráfico aproximado (Nota: dicho gráfico se denomina “curva característica”). |
Punto 5
La recepción de reclamos de clientes en una oficina de TV por cable + Internet puede moldearse según un proceso de Poisson de tasa μ = 18 clientes/hora. Sólo el 35% de los reclamos pueden resolverse. Si un reclamo no puede resolverse, la empresa está obligada a devolver los $200 de cuota pagados por el cliente en el último mes.
| a) | Calcular aproximadamente la probabilidad de que, entre las 10:00 h y las 18:00 h, la empresa tenga que devolver más de %10 000. |
| b) | Con ayuda de una calculadora, simular el tiempo de llegada de los 5 primeros reclamos a partir de las 10:00 h, y el dinero que debe devolver la empresa a causa de todos ellos (deben escribirse todas las variables intermedias obtenidas en la simulación). |
Resolución
Punto 4
Parte a)
Como se trata de eventos binarios e independientes donde la probabilidad es constante, para calcular la probabilidad del número total de discos defectuosos se aplica la distribución binomial.

donde r es la cantidad de defectuosos y n la cantidad total de unidades
En el intervalo ![<tex>r\in\left[2,16\right]</tex> <tex>r\in\left[2,16\right]</tex>](lib/plugins/latex/images/856e31935d2ebe55ff973c70b9f8a06d137cb60f_0.png) hay dos maneras de llegar: la primera es que haya esa cantidad de defectuosos en la primer muestra, y la otra es que haya sólo un defectuoso en la primera y después en la segunda haya
hay dos maneras de llegar: la primera es que haya esa cantidad de defectuosos en la primer muestra, y la otra es que haya sólo un defectuoso en la primera y después en la segunda haya 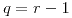 .
.

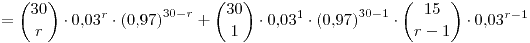


En el caso  , primero debe haber un defectuoso y luego ninguno en la segunda muestra.
, primero debe haber un defectuoso y luego ninguno en la segunda muestra.
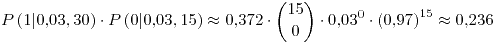
Para los otros r se aplica la distribución binomial normalmente.
![<tex>f\left(r\right)=\begin{cases}\binom{30}r\cdot0.03^r\cdot\left(0.97\right)^{30-r} & \text{ si }r=0\ \ \mathrm{\acute o}\ \ r\in\left[17,30\right] \\ 0.236 & \text{ si } r=1 \\ \binom{30}{r}\cdot 0.03^r\cdot\left(0.97\right)^{30-r}+0.372\cdot \binom{15}{r-1}\cdot 0.03^{r-1}\cdot\left(0.97\right)^{16-r} & \text{ si } 2\leq r\leq 16\end{cases}</tex> <tex>f\left(r\right)=\begin{cases}\binom{30}r\cdot0.03^r\cdot\left(0.97\right)^{30-r} & \text{ si }r=0\ \ \mathrm{\acute o}\ \ r\in\left[17,30\right] \\ 0.236 & \text{ si } r=1 \\ \binom{30}{r}\cdot 0.03^r\cdot\left(0.97\right)^{30-r}+0.372\cdot \binom{15}{r-1}\cdot 0.03^{r-1}\cdot\left(0.97\right)^{16-r} & \text{ si } 2\leq r\leq 16\end{cases}</tex>](lib/plugins/latex/images/30242eeaebdf7cf71ee22a8778d19f4302639b0c_0.png)
Parte b)
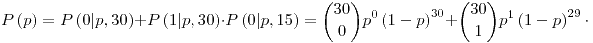

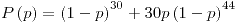
| p | P(p) |
|---|---|
| 0 | 1 |
| 0,025 | 0,714 |
| 0,050 | 0,372 |
| 0,075 | 0,169 |
| 0,100 | 0,071 |
| 0,150 | 0,011 |
| 0,200 | 0,002 |
| 0,300 | 0,000 (aprox.) |
 |  |
| 1 | 0 (exacto) |

