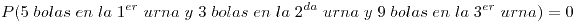GUIA 1

GUIA 1

La enumeracion de los puntos respeta la guia Cederbaum. La enumeracion de la guia comun es el numero en parentasis.

1.1 (1.1)

74% de chicas con cabello oscuro, ojos marrones o ambos; 60% ojos marrones, 70% cabello oscuro.

a) A: ojos marrones B: cabello oscuro P(A U B)= P(A) + P(B) - P(A ∩ B) 0,74 = 0,6 + 0,7 - P(A ∩ B) P(A ∩ B) = 0,56

b) A^c: “Sin ojos marrones” P(B ∩ A^c)= P(B) - P(A ∩ B) = 0,7 - 0,56 = 0,14

c) P(A ∩ B^c) = P (A) - P(A ∩ B = 0,6 - 0,56 = 0,04

d) 1 - P(A U B) = 1 - 0,74 = 0,26

1.24 (1.20)

Este ejercicio se resuelve con el concepto de particiones; en particular usamos coeficientes multinomiales (para más información consultar los apuntes de Grynberg).

Coeficiente Multinomiales: $<tex>\frac {n!}{r_1! \cdot r_2! \cdot \cdot \cdot r_k!}</tex>$ con $<tex>r_1+r_2+...+r_k=n</tex>$

Para ver como se aplica esto vamos a calcular la cantidad de formas que hay para ir del hotel al puerto de pescadores: 14 cuadras separan al hotel del puerto y, como solo puedo moverme hacia la izquierda y hacia abajo, cualquier camino que tome implica caminar 10 cuadras hacia la izquierda y 4 cuadras hacia abajo. Usando Coeficientes Multinomiales nos queda:

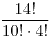$<tex>\frac {14!}{10! \cdot 4!}</tex>$ con $<tex>10+4=14</tex>$ y nos da como resultado $<tex>1001</tex>$ diferentes caminos posibles.

(a) Para calcular la probabilidad de pasar por el quiosco de diarios y revistas yendo del hotel al puerto vamos a resolverlo usando casos favorables sobre casos posibles ya que todos los caminos son igualmente probables:

Casos favorables: $<tex>\frac {5!}{4! \cdot 1!} \cdot \frac {9!}{6! \cdot 3!}</tex>$ y nos da como resultado $<tex>420</tex>$ diferentes caminos posibles. El 1er producto calcula los caminos desde el hotel al quiosco y el 2do producto calcula los caminos del quiosco al puerto.

Casos posibles: ya los calculamos al principio y son $<tex>1001</tex>$

Hacemos la división y nos queda $<tex>\frac {420}{1001} = 0.4196</tex>$

(b) En este punto tenemos una probabilidad condicional ya que nos piden la probabilidad de haber pasado por el quiosco sabiendo que pasó por el café y lo vamos a resolver de la misma manera:

$<tex>P(Q|C) = \frac {P(Q \cap C)}{P(C)} = \frac{50}{120} = 0.4167</tex>$

$<tex>P(Q \cap C) = \frac {5!}{4! \cdot 1!} \cdot \frac {5!}{3! \cdot 2!} = 50</tex>$

$<tex>P(C) = \frac {10!}{7! \cdot 3!} = 120</tex>$

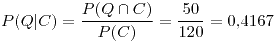
1.25 (1.15 (b))

El modelo estadístico de Bose-Einstein nos dice que un evento particular tiene una probabilidad asociada de 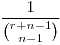$<tex>\frac {1}{{r+n-1 \choose n-1}}</tex>$ siendo $<tex>n</tex>$ el número de urnas y $<tex>r</tex>$ el número de bolas.

(a) Como ambos son eventos particulares tienen asociada la misma probabilidad.

$<tex>P(17 \, bolas \ en \ la \ 1^{er} \ urna) = P(10 \ bolas \ en \ la \ 1^{er} \ urna \ y \ 7 \ bolas \ en \ la \ 2^{da} \ urna) = \frac {1}{{17+20-1 \choose 20-1}} = \frac {1}{{36 \choose 19}} = 1.163 \cdot 10^{-10}</tex>$

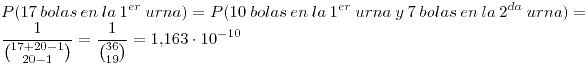
(b) Es un evento particular así que la probabilidad es la misma que en (a)

$<tex>P(Que \ no \ caigan \ bolas \ en \ las \ ultimas \ 3 \ urnas) = \frac {{r+n-1-3 \choose n-1}}{{r+n-1 \choose n-1}} = \frac {{17+20-1-3 \choose 17-1}}{{17+20-1 \choose 20-1}} = </tex>$ $<tex>\frac{{33 \choose 16}}{{36 \choose 19}} = 0.1357</tex>$

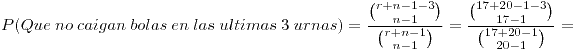
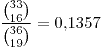
1.26 (No está en la guía de Grynberg)

Nos dicen que tenemos 7 botellas de vino para ubicar en un estante de 4 columnas y 3 filas. Para simplificar la situación podemos pensarlo como un estante de 1 fila y 12 columnas con cada celda numerada del 1 al 12.

Como en cada celda entra a lo sumo una botella y todas las configuraciones son igualmente probables podemos aplicar la estadística de Fermi-Dirac para resolver el ejercicio.

Para calcular la probabilidad de que la fila de arriba quede ocupada podemos pensarlo como si las celdas del 1 al 4 estuvieran llenas con una botella cada una lo cual implicaría que habría que repartir las 3 botellas que quedan en las celdas que van del 5 al 12. Por lo tanto estamos en una situación de casos favorables sobre casos posibles donde:

Casos favorables: $<tex>{8 \choose 3}=56</tex>$

Casos posibles: 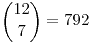$<tex>{12 \choose 7}=792</tex>$

Hacemos la división y nos queda 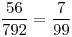$<tex>\frac {56}{792} = \frac{7}{99}</tex>$

1.30 (1.15 (a) y (c))

(a) El modelo estadístico de Maxwell-Boltzmann nos dice que un evento particular tiene una probabilidad asociada de 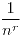$<tex>\frac {1}{n^{r}}</tex>$ siendo $<tex>n</tex>$ el número de urnas y $<tex>r</tex>$ el número de bolas.

$<tex>P(17 \, bolas \ en \ la \ 1^{er} \ urna) = \frac {{17 \choose 17}}{20^{17}} = 7.6 \cdot 10^{-23}</tex>$

$<tex>P(10 \ bolas \ en \ la \ 1^{er} \ urna \ y \ 7 \ bolas \ en \ la \ 2^{da} \ urna) = \frac {{17 \choose 10} \cdot {7 \choose 7}}{20^{17}} = 1.48 \cdot 10^{-18}</tex>$

Las probabilidades calculadas son iguales.

$<tex>P(5 \ bolas \ en \ la \ 1^{er} \ urna \ y \ 3 \ bolas \ en \ la \ 2^{da} \ urna \ y \ 9 \ bolas \ en \ la \ 3^{er} \ urna) = </tex>$ $<tex>\frac {{17 \choose 5} \cdot {12 \choose 3} \cdot {9 \choose 9}}{20^{17}} = 1.03 \cdot 10^{-16}</tex>$

$<tex>P(Que \ no \ caigan \ bolas \ en \ las \ ultimas \ 3 \ urnas) = \frac{(n-3)^r}{n^r} = \frac{(20-3)^{17}}{20^{17}} = </tex>$ $<tex>\frac{17^{17}}{20^{17}} = 0.0631</tex>$

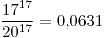
© El modelo estadístico de Fermi-Dirac nos dice que un evento particular tiene una probabilidad asociada de $<tex>\frac {1}{{n \choose r}}</tex>$ siendo $<tex>n</tex>$ el número de urnas y $<tex>r</tex>$ el número de bolas.

$<tex>P(17 \, bolas \ en \ la \ 1^{er} \ urna) = 0 </tex>$

$<tex>P(10 \ bolas \ en \ la \ 1^{er} \ urna \ y \ 7 \ bolas \ en \ la \ 2^{da} \ urna) = 0 </tex>$

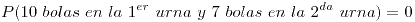
Las probabilidades calculadas no son iguales.

$<tex>P(5 \ bolas \ en \ la \ 1^{er} \ urna \ y \ 3 \ bolas \ en \ la \ 2^{da} \ urna \ y \ 9 \ bolas \ en \ la \ 3^{er} \ urna) = 0 </tex>$

$<tex>P(Que \ no \ caigan \ bolas \ en \ las \ ultimas \ 3 \ urnas) = \frac {{(n-3) \choose r}}{{n \choose r}} = \frac {{(20-3) \choose 17}}{{20 \choose 17}} = \frac {{17 \choose 17}}{{20 \choose 17}} = </tex>$ $<tex> 0.000877 </tex>$

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.