Examen Final - 61.06 Probabilidad y Estadística A (Industrial) - 08/08/2007
Cátedra: Común a todas (me parece que fue hecho por Cederbaum porque había ejercicios teóricos)
Fecha: 5º Oportunidad - 1º Cuatrimestre 2007
Día: 08/08/2007
Enunciado
Punto 1
Se genera un número random  y luego un segundo número random
y luego un segundo número random 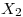 independiente del anterior.
independiente del anterior.
Sea 
Encontrar:

Punto 2
Una empresa constructora de caminos tiene capacidad para nivelar un promedio de 250 metros por ruta (distancia exponencial). En los días de lluvia no es posible trabajar, siendo la probabilidad diaria de lluvia del 20%. Obtener la probabilidad de que en los próximos 4 días se nivelen más de 800 metros (dejar expresado claramente el cálculo).
Punto 3
El tiempo que un operario tarda en realizar la operación A es 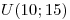 . El tiempo para la operación B es
. El tiempo para la operación B es  . Si 2 operarios comienzan simultáneamente dichas operaciones, ¿cuál es la probabilidad de que las operaciones terminen con menos de un minuto de diferencia?
. Si 2 operarios comienzan simultáneamente dichas operaciones, ¿cuál es la probabilidad de que las operaciones terminen con menos de un minuto de diferencia?
Punto 4
Demostrar mediante operaciones en un espacio bidiscreto, que la suma de dos variables aleatorias Poisson independientes genera una nueva variable Poisson. ¿Existe alguna restricción para el valor de cada  ?
?
Punto 5
Sea 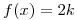 en el intervalo
en el intervalo 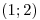 ;
; 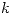 en el intervalo
en el intervalo  ; nula para el resto.
; nula para el resto.
Sea  en el intervalo
en el intervalo  ;
;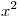 en el intervalo
en el intervalo  . Encontrar
. Encontrar  y graficar.
y graficar.
Resolución
Punto II
Defino:
 : cantidad de metros nivelados por día.
: cantidad de metros nivelados por día.
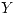 : número de días trabajados.
: número de días trabajados.
Para resolver el problema hay que utilizar la propiedad que la suma de  variables Exponenciales con misma media, es una variable Gamma de parámetro
variables Exponenciales con misma media, es una variable Gamma de parámetro  . Es decir:
. Es decir:
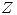 : cantidad total de metros nivelados.
: cantidad total de metros nivelados.

En nuestro caso 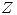 tiene distribución Gamma con parámetro
tiene distribución Gamma con parámetro  .
.
Necesito calcular el  de la distribución exponencial. Tengo como dato:
de la distribución exponencial. Tengo como dato:

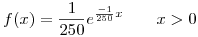
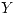 tiene distribución binomial, ya que hay dicotomía, probabilidad constante e independencia. Considero éxito que se pueda trabajar (es decir, que no llueva).
tiene distribución binomial, ya que hay dicotomía, probabilidad constante e independencia. Considero éxito que se pueda trabajar (es decir, que no llueva).

Ahora existen varias maneras de buscar la solución al problema, pero ya está hecho lo más importante. Un camino fácil es dividir el problema en cinco casos posibles:
- 0 días de trabajo
- 1 día de trabajo
- 2 días de trabajo
- 3 días de trabajo
- 4 días de trabajo
De acuerdo a la cantidad de días que se trabajen, 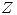 será una Gamma con parámetro distinto:
será una Gamma con parámetro distinto:

El enunciado me pide:
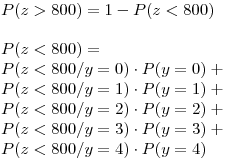
Como sólo hay que dejar planteado el cálculo, no hace falta hacer las cuentas, pero si alguien quiere agregarlas estaría bueno porque de paso sirven para practicar el uso de la tabla.
Punto III
 : “tiempo que tarda en realizar la operacion A“
: “tiempo que tarda en realizar la operacion A“
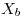 : “tiempo que tarda en realizar la operacion B“
: “tiempo que tarda en realizar la operacion B“



Que las operaciones terminen con menos de 1 minuto de diferencia:

El modulo es porque puede terminar primero A o primero B, hay que tener en cuenta los 2 casos.

Ahora hay que hacer el grafico, el dominio inicial era Xa entre 10 y 15; Xb entre 12 y 16. Para calcular la probabilidad hay que integrar, dentro del dominio, entre Xa+1 y Xa-1. Haciendo el grafico se ve mejor.


