Examen Final - 61.06 Probabilidad y Estadística A - No Industrial
Cátedra: Todas
Fecha: 2º Oportunidad - Invierno 2006
Día: 12/07/2006
Enunciado
Punto I
La distribución conjunta de x e y es una variable uniforme con dominio circular en el plano xy. Obtener el valor del coeficiente de correlación e interpretar el resultado (se puede resolver el ejercicio conceptualmente, sin hacer el cálculo).
Punto II
Encontrar la función de probabilidad de la suma de la V.A.X., binomial (n=1,p=0.5); con la V.A.Y., binomial (n=2, p=0.9) e indicar si se obtiene una nueva distribución binomial. (en caso afirmativo indique la relación entre los parámetros)
Punto III
Sea X una V.A. que representa una magnitud que se quiere medir en un proceso de producción. Su f.d.p. es:
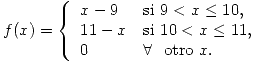
Si se desea controlar que la media de la variable x se mantenga a lo sumo en 10 con 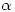 = 0.05. Calcular
= 0.05. Calcular
- Zona de aceptación y rechazo y curva característica de operación si se toma como variable de control una sola muestra.
- Idem anterior si la variable de control es la media muestral con n= 50.
Punto IV
En un depósito hay 40000 piezas para analizar grado de deterioro de las mismas, se toma una muestra al azar de 800 piezas encontrando 2 piezas muy deterioradas. Si el costo de reparación de c/ pieza deteriorada es $300, ¿cuál es el monto mínimo que con 98% de prob. deberá presupuestarse para la reparación del total de las piezas del depósito?
Punto V
La cantidad de reactivo que se consume en cada operación industrial tiene una distribución uniforme U(0;2) en kg. La cantidad de operaciones por hora tiene una distribución binomial (n=2; p= 0.75). Calcular la probabilidad de que en una hora se consuman menos de 1.5 kg del reactivo
Resolución
Punto I
Punto II
La suma de X e Y no es normal porque tiene diferente p. Para hacer la suma se debe hacer en un cuadro.
| X | |||
| 0 | 1 | ||
| 0 | 0.05 | 0.05 | |
| Y | 1 | 0.09 | 0.09 |
| 2 | 0.405 | 0.405 |
Viendo los distintos valores que puede tomar 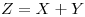 .
.

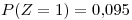

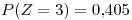
Punto III
Hago la primer parte nomás.


Se toma una sola muestra, entonces la variable a controlar es X.
Se toma un 
Si 
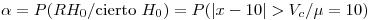
Si se dibuja esto en un gráfico, se ve que esta última probabilidad es dos veces el área de un triángulo de altura 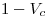 y base igual. Por lo tanto:
y base igual. Por lo tanto:

Por lo tanto si 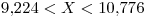 se acepta la hipótesis para la media de X.
se acepta la hipótesis para la media de X.
La CCO debe hallarse para cada 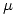 en particular. [PENDIENTE]
en particular. [PENDIENTE]
Punto IV
Se estima la proporción de deterioradas como 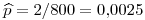 .
.
Como para tantos valores  es una normal de media
es una normal de media  y
y  , donde
, donde 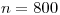 .
.
Entonces: 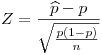
Entonces: 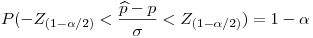
Como quiero la proporción con 98% de confianza, 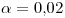 .
.
El fractil es  .
.
Como no se puede despejar p, se aproxima el desvio estándar los valores de p con los valores estimados, entonces:  .
.
Entonces:  .
.
 . ⇐ Es el IC para p.
. ⇐ Es el IC para p.
El presupuesto se obtendrá con el mayor p, (para cubrir todo el intervalo). 
Por lo tanto habrá 265 piezas falladas, y el presupuesto necesario será de al menos $79500.
Punto V
X: cantidad de ractivo en cada operación → U(0;2)
Y: cantidad de operaciones por hora → Bi(n=2; p=0.75)
Z: cantidad de reactivo en una hora

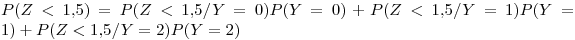
Las probabilidades de Y se calculan con la binomial, y dan:

Las otras probabilidades son:
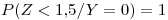 porque no se puede haber gastado reactivo sin operar.
porque no se puede haber gastado reactivo sin operar.


Esta probabilidad se calcula viendo que si  y
y 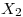 son independientes,
son independientes,  (se multiplican las funciones).
(se multiplican las funciones).
Se resuelve haciendo la integral (o viendo el área directamente): 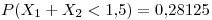 .
.
Haciendo la cuenta total se obtiene:  .
.
Por lo tanto, hay un 50,19% de probabilidad de gastar menos de 1,5kg por hora de reactivo.
