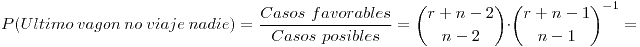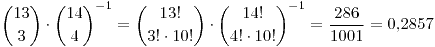Primer Parcial (Primer Recuperatorio) - 61.06 Probabilidad y Estadística A
Cátedra: Cederbaum
Fecha: Primer Parcial - Primer Recuperatorio- 2° Cuatrimestre
Día: 18/11/2011
Ejercicio 1
Cada integrante de un matrimonio habla por mes una cantidad de minutos aleatorias independiente distribuida uniformemente en el intervalo 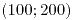 y se hace una factura conjunta. El precio del minuto depende de la cantidad hablada: si entre los dos suman menos de
y se hace una factura conjunta. El precio del minuto depende de la cantidad hablada: si entre los dos suman menos de 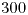 minutos cuesta
minutos cuesta 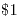 el minuto, pero si superan los
el minuto, pero si superan los 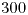 minutos se les factura el minuto
minutos se les factura el minuto 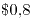 . Calcular la probabilidad de que la factura tenga un importe entre
. Calcular la probabilidad de que la factura tenga un importe entre 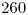 y
y 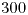 pesos.
pesos.
Ejercicio 2
Una persona lee por día una cantidad de páginas aleatorias con Media 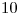 y Desvío Estándar
y Desvío Estándar 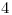 . Al comenzar un mes de
. Al comenzar un mes de  días la persona desea elegir un libro de tal forma que tenga una probabilidad de
días la persona desea elegir un libro de tal forma que tenga una probabilidad de 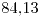 por ciento de terminarlo en dicho mes. ¿Cuantas hojas debe tener el libro como máximo?
por ciento de terminarlo en dicho mes. ¿Cuantas hojas debe tener el libro como máximo?
Ejercicio 3
En cada punto de un partido de ping-pong la cantidad de veces que la pelota pasa la red es una variable aleatoria  que se distribuye así:
que se distribuye así: 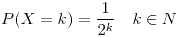
Si la pelota pasa menos de 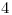 veces una persona que mira el partido no aplaude ninguna vez. Si pasa
veces una persona que mira el partido no aplaude ninguna vez. Si pasa 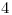 o más veces la cantidad de aplausos es
o más veces la cantidad de aplausos es 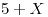
a) Hallar la función de probabilidad de la cantidad de aplausos.
b) Sabiendo que hubo aplausos, calcular la probabilidad de que la pelota haya pasado más de  veces.
veces.
Ejercicio 4
Diez personas esperan un tren de cinco vagones en la estación. Si las personas son indistinguibles y todas las configuraciones son equiprobables:
a) ¿Cuál es la probabilidad de que vayan  a cada vagón?
a cada vagón?
b) ¿Cuál es la probabilidad de que en el último vagón no viaje nadie?
Ejercicio 5
Los tiempos en que dos procesadores  e
e 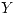 calculan el decimal n°
calculan el decimal n°  de
de  son variables aleatorias independientes exponenciales de parámetros
son variables aleatorias independientes exponenciales de parámetros  y
y  segundos respectivamente. Hallar la probabilidad de que el segundo procesador haya terminado antes sabiendo que la suma de los tiempos de ambos fue menor a
segundos respectivamente. Hallar la probabilidad de que el segundo procesador haya terminado antes sabiendo que la suma de los tiempos de ambos fue menor a  segundos.
segundos.
Discusión
Ejercicio 1
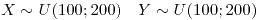
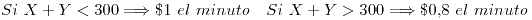
La función densidad conjunta es una constante y se calcula como 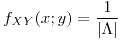 siendo
siendo 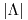 el soporte de la región y vale
el soporte de la región y vale 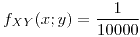 . Al ser constante vamos a poder resolver este ejercicio como áreas favorables sobre área posible siendo el área posible
. Al ser constante vamos a poder resolver este ejercicio como áreas favorables sobre área posible siendo el área posible  .
.
Ahora calculamos las áreas favorables. Tenemos 2 áreas que calcular:
La 1ra es las más fácil y es el trapecio comprendido entre las rectas 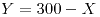 e
e 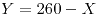 y lo calculamos haciendo la diferencia entre el triángulo grande y el triángulo chico y nos da
y lo calculamos haciendo la diferencia entre el triángulo grande y el triángulo chico y nos da 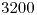 .
.
La 2da es más difícil ya que tenemos que pasar los datos que están en pesos a minutos:
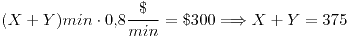
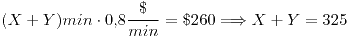
El área favorable es el trapecio formado por estas 2 rectas y lo calculo de la misma manera que antes y da 
Ahora que tengo todos los datos resuelvo:
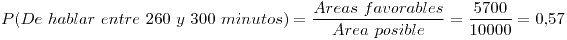
Ejercicio 2
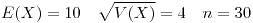
Como  es bastante grande puedo armar una función normal.
es bastante grande puedo armar una función normal.
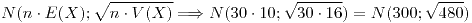
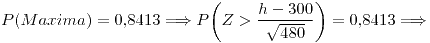
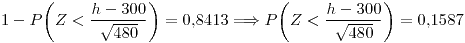


Ejercicio 3
Ejercicio 4
Estamos en un clásico ejercicio de bolas y urnas donde las personas juegan el rol de las bolas y los vagones juegan el rol de las urnas. Como las personas (bolas) son indistinguibles y todas las configuraciones son equiprobables estamos en una situación de Mecánica Estadísitica de Bose-Einstein.
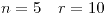
a)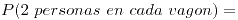
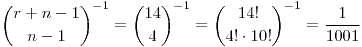
b) La forma de resolver esta parte es pensarlo como casos favorables sobre casos posibles siendo los casos favorables la distribución de 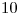 personas en
personas en  vagones y los casos posibles igual que el punto anterior.
vagones y los casos posibles igual que el punto anterior.