Versión de la guía: Agosto 2010
Post en el Foro
Pueden descargar la versión pdf desde este link. Sin embargo, puede estar desactualizada puesto que no se edita más.
Es posible buscar cada ejercicio según su numeración, con la excepción de la guía 1. Por ejemplo, en el caso de que quieran ver el resultado del ejercicio 12 de la guía 8, ingresan en el buscador del navegador lo siguiente: 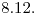 . Para la guía 10 hay que escribir 0 en lugar de 10. Ejemplo de guía 10, ejercicio 16:
. Para la guía 10 hay que escribir 0 en lugar de 10. Ejemplo de guía 10, ejercicio 16: 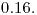
| 4.1. |
| (a) |

Dominio:  |
| (b) |

 |
| (c) |
 |
| (d) |
Las funciones  y y  son diferenciables en son diferenciables en 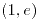 , por la tanto la composición , por la tanto la composición 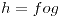 también es diferenciable en también es diferenciable en 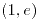 . . |
|
| 4.2. |
| (a) |
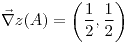 |
| (b) |
 |
|
| 4.3. |
Dirección: 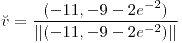 . Valor: . Valor: 
 Falta justificar Falta justificar |
| 4.4. |
- |
| 4.5. |
- |
| 4.6. |
|
| 4.7. |
- |
| 4.8. |

Existe el plano tangente porque la función  es diferenciable en es diferenciable en  |
| 4.9. |
- |
| 4.10. |
| (a) |
 |
| (b) |
- |
|
| 4.11. |
| (a) |

Función:  |
| (b) |

Función:  |
| (c) |

Función:  |
| (d) |
- |
|
| 4.12. |
| (a) |
 |
| (b) |
 |
|
| 4.13. |
 |
| 4.14. |
|
| 4.15. |
Las derivadas cruzadas resultan iguales porque se cumplen las hipótesis del teorema de Schwarz.
|
| 4.16. |
Conjunto de puntos: FALTA
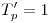 , , 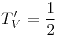 |
| 4.17. |
- |
| 4.18. |
|
| 4.19. |
|
| 4.20. |
 |
| 4.21. |
- |
| 4.22. |
 |
| 4.23. |
 |
| 5.1. |
| (a) |
 |
| (b) |
 |
|
| 5.2. |
 |
| 5.3. |
|
| 5.4. |
 |
| 5.5. |
 |
| 5.6. |
 |
| 5.7. |
Punto crítico : sea 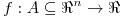 . A los puntos . A los puntos 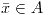 en los que podría haber extremos se los llama puntos críticos. en los que podría haber extremos se los llama puntos críticos.
Hay de dos tipos:
Puntos donde  no es diferenciable. Puntos estacionarios: puntos donde  es derivable y  .
#
Sea 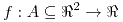 una función definida en el conjunto abierto una función definida en el conjunto abierto  de de 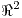 : :
Mínimo relativo : se dice que  tiene un mínimo relativo en el punto tiene un mínimo relativo en el punto 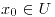 si si  . .
Máximo relativo : se dice que  tiene un máximo relativo en el punto tiene un máximo relativo en el punto 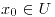 si si  . .
Punto silla : si un entorno de 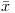 contiene puntos contiene puntos  tales que tales que 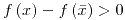 y puntos y puntos  tales que tales que 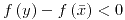 se dice que se dice que 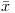 es un punto silla de la función es un punto silla de la función  . . |
| 5.8. |
Sea 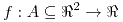 una función definida en el conjunto abierto una función definida en el conjunto abierto  de de 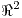 : :
Mínimo absoluto : se dice que  tiene un mínimo absoluto en el punto tiene un mínimo absoluto en el punto 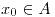 si si 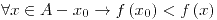 . .
Máximo absoluto :se dice que  tiene un máximo absoluto en el punto tiene un máximo absoluto en el punto 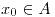 si si 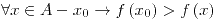 . . |
| 5.9. |
- |
| 5.10. |
Si. |
| 5.11. |
| (a) |
Punto silla en  |
| (b) |
Mínimo en 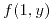 y y  |
| (c) |
No existen extremos |
| (d) |
Máximo en  |
| (e) |
Máximo en  y mínimo en y mínimo en  |
| (f) |
Mínimo en  |
|
| 5.12. |
| (a) |
Mínimo en 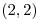 , puntos silla en , puntos silla en 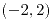 y y  , máximo en , máximo en  |
| (b) |
Mínimo en los puntos de la recta  |
| (c) |
Mínimo en  |
| (d) |
Punto silla en  |
| (e) |
Mínimo en 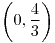 , puntos silla en , puntos silla en  y y 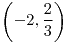 , máximo en , máximo en  |
| (f) |
Máximo en  , puntos silla en , puntos silla en  |
|
| 5.13. |
Ninguna función tiene un máximo en ese punto crítico.
| (a) |
 |
| (b) |
![<tex>k \in [-2,2]</tex> <tex>k \in [-2,2]</tex>](lib/plugins/latex/images/1db457a047d73a6d7a4e8a1bd9d652de9ea4cbf1_0.png) |
|
| 5.14. |
| (a) |
Mínimo en 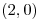 , puntos silla en , puntos silla en  y y  , máximo en , máximo en  |
| (b) |
Mínimo en 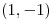 , máximo en , máximo en  |
| (c) |
Mínimo en 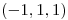 , máximo en , máximo en  |
| (d) |
Máximo en  , punto silla en , punto silla en  para para  |
| (e) |
Mínimo en 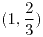
|
|
 Faltan los ejercicios 16 a 26
Faltan los ejercicios 16 a 26
En el siguiente enlace se encuentra la guía resuelta en su totalidad (a excepción del ejercicio 17) por Fernando Acero y Jorge Comas:
tpVI.htm
Incluye applets y un archivo pdf para imprimir. Observar que el ejercicio 17 fue agregado en el segundo cuatrimestre del 2010 y por lo tanto los ejercicios 18 y 19 de la guía aparecen como si fuesen los ejercicios 17 y 18, respectivamente.
| 7.1. |
| (a) |
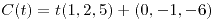 con con 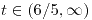 . Es simple. . Es simple.
 |
| (b) |
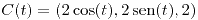 con con  . Es simple. . Es simple.
 |
| (c) |
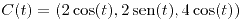 con con ![<tex>t\in[0,\pi /2]</tex> <tex>t\in[0,\pi /2]</tex>](lib/plugins/latex/images/92580d77a6439bc45e47009e39265b9e4b75b20c_0.png) . Es simple. . Es simple.
 |
| (d) |
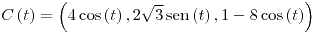 con con ![<tex>t\in\left[0,2\pi\right]</tex> <tex>t\in\left[0,2\pi\right]</tex>](lib/plugins/latex/images/4aea26cd58169211ffb410396debef3f51404407_0.png) . Es simple. . Es simple.
 |
|
| 7.2. |
Son las mismas que el ejercicio anterior, invirtiendo el orden del intervalo de t.
| (a) |
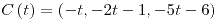 con con  |
| (b) |
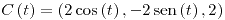 con con ![<tex>t\in\left[0,2\pi\right]</tex> <tex>t\in\left[0,2\pi\right]</tex>](lib/plugins/latex/images/4aea26cd58169211ffb410396debef3f51404407_0.png) |
| (c) |
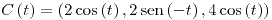 con con ![<tex>t\in\left[-\frac{\pi}{2},0\right]</tex> <tex>t\in\left[-\frac{\pi}{2},0\right]</tex>](lib/plugins/latex/images/1258c1ca911b3200a7698d790fcfd4c772aee271_0.png) |
| (d) |

con ![<tex>t\in\left[0,2\pi\right]</tex> <tex>t\in\left[0,2\pi\right]</tex>](lib/plugins/latex/images/4aea26cd58169211ffb410396debef3f51404407_0.png) |
|
| 7.3. |
| (a) |
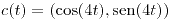 , con , con ![<tex>t\in[0,\pi /2]</tex> <tex>t\in[0,\pi /2]</tex>](lib/plugins/latex/images/92580d77a6439bc45e47009e39265b9e4b75b20c_0.png) |
| (b) |
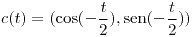 , con , con ![<tex>t\in[0,4\pi]</tex> <tex>t\in[0,4\pi]</tex>](lib/plugins/latex/images/a6382e72a9ef9cddaa16b05c74622dd71725c9b5_0.png) |
| (c) |
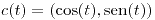 con con  |
|
| 7.4. |
| (a) |
Longitud: 
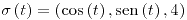 con con ![<tex>t\in\left[0,2\pi\right]</tex> <tex>t\in\left[0,2\pi\right]</tex>](lib/plugins/latex/images/4aea26cd58169211ffb410396debef3f51404407_0.png)
 |
| (b) |
Longitud: 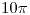
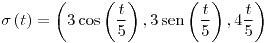 con con ![<tex>t\in\left[0,10\pi\right]</tex> <tex>t\in\left[0,10\pi\right]</tex>](lib/plugins/latex/images/e56e637f506345c06c5baf8be9a7cdf554c27f33_0.png)
Recta tangente: 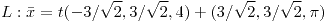
Plano normal:  |
| (c) |
12 ¿?
 |
|
| 7.5. |
| (a) |
 |
| (b) |
 |
|
| 7.6. |
| (a) |
 |
| (b) |
 |
| (c) |
 |
| (d) |
Masa: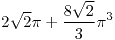
Densidad media: 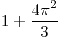
Centro de masa:  |
| (e) |
 |
| (f) |
3 |
|
| 7.7. |
| (a) |
0 |
| (b) |
 |
|
| 7.8. |
| (a) |
1 |
| (b) |
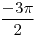 |
|
| 7.9. |
| (a) |
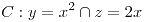

Circulación: 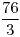
Punto inicial: (0,0,0)
Punto final: (2,4,4) |
| (b) |
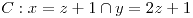

Circulación: 54
Punto inicial: (0,-1,-1)
Punto final: (3,5,2) |
|
| 7.10. |
| (a) |
Si. 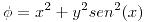 |
| (b) |
No. |
| (c) |
Si.  |
| (d) |
No. |
|
| 7.11. |
| (a) |
El jacobiano de F no es simétrico:  |
| (b) |
 ó 1/3 (comprobar) ó 1/3 (comprobar) |
|
| 7.12. |
| (a) |
 |
| (b) |
Son paraboloides elípticos. |
| (c) |
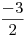 |
|
| 7.13. |
| (a) |
 |
| (b) |
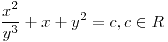 |
| (c) |
 |
| (d) |
 |
| (e) |
 |
| (f) |
 |
| (g) |
 |
|
| 7.14. |
| (a) |
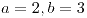 . .
Dominio: 
Circulación:  |
| (b) |
 |
| (c) |
En sentido horario:  |
|
| 7.15. |
 |
| 7.16. |
4 |
| 7.17. |
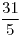 |
| 7.18. |
|
| 7.19. |
| (a) |
 |
| (b) |
 |
|
| 7.20. |
|
| 7.21. |
20 |
| 7.22. |
1 |
| 7.23. |
|
| 7.24. |
- |
| 7.25. |
|
| 7.26. |
|
| 7.27. |
- |
| 7.28. |
 |
| 8.1. |
| (a) |

 |
| (b) |
1
 |
| (c) |
 ó 1/2 (comprobar) ó 1/2 (comprobar) 
 |
| (d) |
32
 |
| (e) |
3
 |
| (f) |

 |
|
| 8.2. |
|
| 8.3. |
Masa: 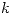
Centro de masa:  |
| 8.4. |
Centro de masa:  |
| 8.5. |
| (a) |
 |
| (b) |
0 |
| (c) |
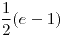 |
| (d) |
0 |
|
| 8.6. |
|
| 8.7. |
|
| 8.8. |
| (a) |
 |
| (b) |
2 |
| (c) |
 |
|
| 8.9. |
 |
| 8.10. |
 |
| 8.11. |
| (a) |
 |
| (b) |
 |
| (c) |
 |
| (d) |
 |
| (e) |
 |
| (f) |
 |
| (g) |
 |
|
| 8.12. |
|
| 8.13. |
| (a) |
 |
| (b) |
 |
| (c) |
Faltan datos en el enunciado |
| (d) |
 |
| (e) |
 |
|
| 8.14. |
- |
| 8.15. |
 |
| 8.16. |
 |
| 8.17. |
 |
| 8.18. |
 |
| 8.19. |
Conviene con esféricas. Integral:  |
| 8.20. |
 , puntos silla en , puntos silla en 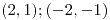 , máximo en , máximo en 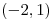 , mínimo en , mínimo en  |
| 8.21. |
| (a) |
0 |
| (b) |
 |
| (c) |
 |
|
| 9.1. |
|
| 9.2. |
 |
| 9.3. |
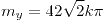 (No estoy segura) (No estoy segura)  |
| 9.4. |
0 |
| 9.5. |
 |
| 9.6. |
| (a) |
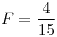 , con normal saliente , con normal saliente |
| (b) |
 |
| (c) |
 |
| (d) |
 , con normal saliente, no estoy segura , con normal saliente, no estoy segura  |
|
| 9.7. |
 |
| 9.8. |
 |
| 9.9. |
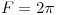 , con normal saliente , con normal saliente |
| 9.10. |
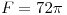 , con normal hacia arriba , con normal hacia arriba |
| 9.11. |
 |
| 9.12. |
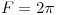 , no estoy segura si es + o - , no estoy segura si es + o -  |
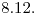 . Para la guía 10 hay que escribir 0 en lugar de 10. Ejemplo de guía 10, ejercicio 16:
. Para la guía 10 hay que escribir 0 en lugar de 10. Ejemplo de guía 10, ejercicio 16: 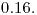
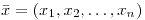
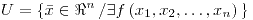
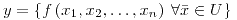
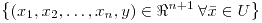
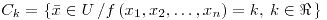
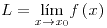 si para cualquier
si para cualquier 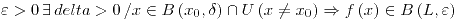
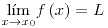
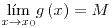
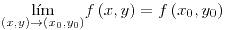
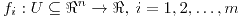 deben ser continuas
deben ser continuas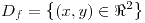
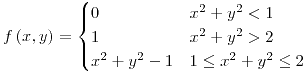
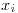 ):
): 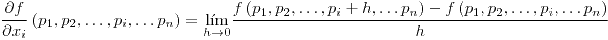
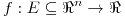 ,
, 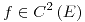 y
y 
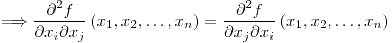
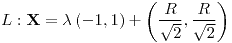

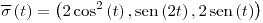 , con
, con ![<tex>t\in\left[0,2\pi\right]</tex> <tex>t\in\left[0,2\pi\right]</tex>](lib/plugins/latex/images/4aea26cd58169211ffb410396debef3f51404407_0.png)
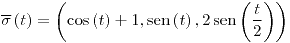 , con
, con ![<tex>t\in\left[-2\pi,2\pi\right]</tex> <tex>t\in\left[-2\pi,2\pi\right]</tex>](lib/plugins/latex/images/bf4d99498d4b6e0183e1e4aadeb2671d751395d4_0.png)
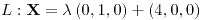
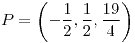
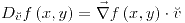 porque las funciones son diferenciables:
porque las funciones son diferenciables: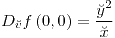 (derivadas en todas las direcciones ¿
(derivadas en todas las direcciones ¿ ?)
?)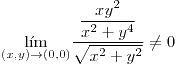
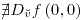 !¿?!
!¿?!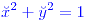


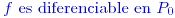
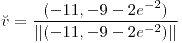 . Valor:
. Valor: 
 Falta justificar
Falta justificar
 es diferenciable en
es diferenciable en 

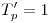 ,
, 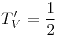







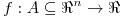 . A los puntos
. A los puntos 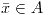 en los que podría haber extremos se los llama puntos críticos.
en los que podría haber extremos se los llama puntos críticos.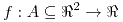 una función definida en el conjunto abierto
una función definida en el conjunto abierto  de
de 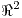 :
: tiene un mínimo absoluto en el punto
tiene un mínimo absoluto en el punto 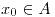 si
si 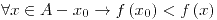 .
. tiene un máximo absoluto en el punto
tiene un máximo absoluto en el punto 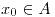 si
si 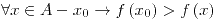 .
. Faltan los ejercicios 16 a 26
Faltan los ejercicios 16 a 26

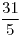

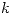









 , puntos silla en
, puntos silla en 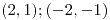 , máximo en
, máximo en 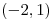 , mínimo en
, mínimo en 

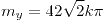 (No estoy segura)
(No estoy segura) 



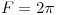 , con normal saliente
, con normal saliente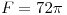 , con normal hacia arriba
, con normal hacia arriba
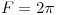 , no estoy segura si es + o -
, no estoy segura si es + o - 
 ,
,  . Hipótesis:
. Hipótesis: 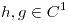
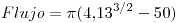 , versor normal saliente.
, versor normal saliente. , versor normal saliente.
, versor normal saliente.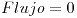
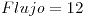
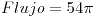
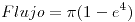
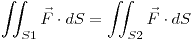
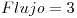
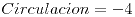
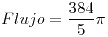
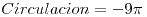
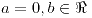



 ; si
; si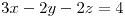 ; si
; si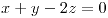 ; no
; no
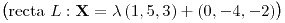
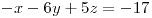 ; si
; si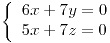 ; si
; si
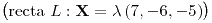
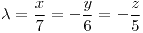
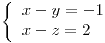 ; si
; si
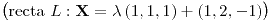
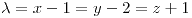
 ; si
; si
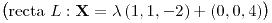
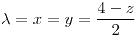

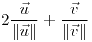
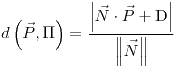 ;
; 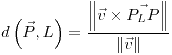
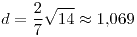
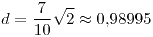
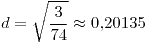
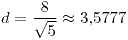
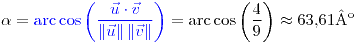
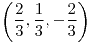
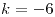 ;
; 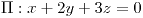

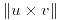

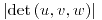




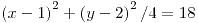



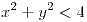
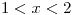 ;
; 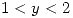 ó
ó 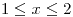 ;
; 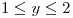
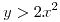
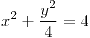 ó
ó 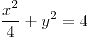


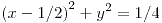 ;
; 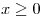 ;
; 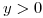

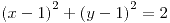

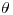 en los ítems (e) y (f), porque el radio nunca puede ser negativo (
en los ítems (e) y (f), porque el radio nunca puede ser negativo (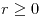 )
)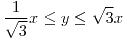

 ;
; 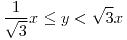

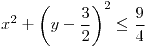
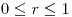
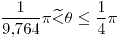
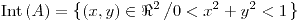
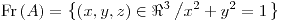
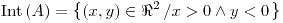
![<tex>\text{Fr}\left(A\right)=\begin{array}[t]{l} \left\{ \left(x,y\right)\in \Re^{2}\left/\left(x=0\wedge y\leq0\right)\right.\right.\\ \left.\vee\left(x\geq0\wedge y=0\right)\right\} \end{array}</tex> <tex>\text{Fr}\left(A\right)=\begin{array}[t]{l} \left\{ \left(x,y\right)\in \Re^{2}\left/\left(x=0\wedge y\leq0\right)\right.\right.\\ \left.\vee\left(x\geq0\wedge y=0\right)\right\} \end{array}</tex>](lib/plugins/latex/images/a1c74f44c11113353bbfbd94d7ddb0e071fc62b7_0.png)
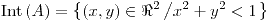
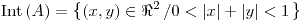
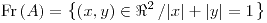
![<tex>\text{Fr}\left(A\right)=\begin{array}[t]{l} \left\{ \left(x,y\right)\in \Re^{2}\left/x^{2}+y^{2}+z^{2}=1\right.\right.\\ \left.\vee\left(x\geq0\wedge y=0\right)\right\} \end{array}</tex> <tex>\text{Fr}\left(A\right)=\begin{array}[t]{l} \left\{ \left(x,y\right)\in \Re^{2}\left/x^{2}+y^{2}+z^{2}=1\right.\right.\\ \left.\vee\left(x\geq0\wedge y=0\right)\right\} \end{array}</tex>](lib/plugins/latex/images/b097b17fa81f4977749276e1b9b0b296073e6ce9_0.png)

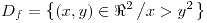
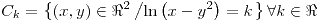



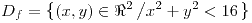
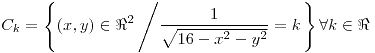

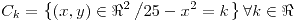

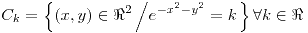

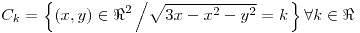

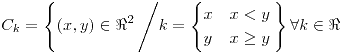

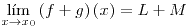

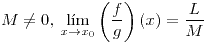
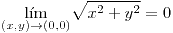

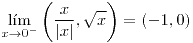
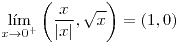

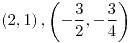
 y
y  son curvas pertenecientes al gráfico de
son curvas pertenecientes al gráfico de  y
y  :
: 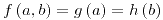
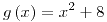 ;
; 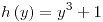
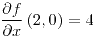 ;
; 
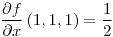 ;
; 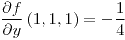 ;
; 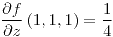
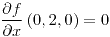 ;
; 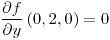 ;
; 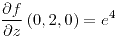
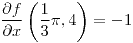 ;
; 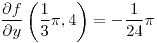
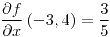 ;
; 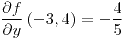
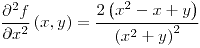
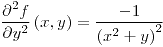
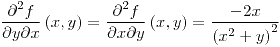
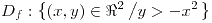
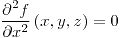 ;
; 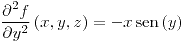
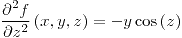
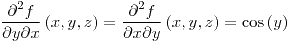
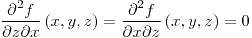
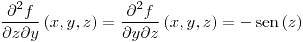
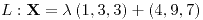 ;
;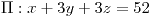
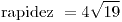
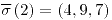 ;
; 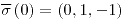

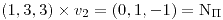
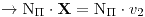
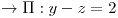
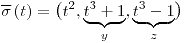
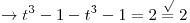
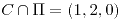
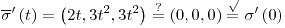
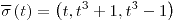 ,
, 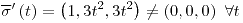

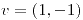 cuando
cuando 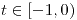
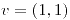 cuando
cuando ![<tex>t\in\left(0,-1\right]</tex> <tex>t\in\left(0,-1\right]</tex>](lib/plugins/latex/images/8ca309e162e62fb9cc4c4f3dd873e945a0e385db_0.png)
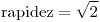

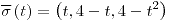 ;
; 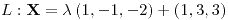
![<tex>\overline{\sigma}\left(t\right)=\left\{ \begin{array}{l} \left(\cos\left(t\right),\sen\left(t\right),1\right)\text{, con }t\in\left[0,2\pi\right]\\ \left(t,\sqrt{1-t^{2}},1\right)\text{, con }t\in\left[-1,1\right] \end{array}\text{o}\right.</tex> <tex>\overline{\sigma}\left(t\right)=\left\{ \begin{array}{l} \left(\cos\left(t\right),\sen\left(t\right),1\right)\text{, con }t\in\left[0,2\pi\right]\\ \left(t,\sqrt{1-t^{2}},1\right)\text{, con }t\in\left[-1,1\right] \end{array}\text{o}\right.</tex>](lib/plugins/latex/images/a8943410bd7e3ac895c1090e5f1b1e995bb70411_0.png)

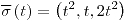 ;
; 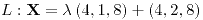
![<tex>\overline{\sigma}\left(t\right)=\left\{ \begin{array}{l} \left(\sqrt{2}\cos\left(t\right),\sqrt{2}\sen\left(t\right),2\right)\text{, con }t\in\left[0,2\pi\right]\\ \left(t,\sqrt{2-t^{2}},2\right)\text{, con }t\in\left[-\sqrt{2},\sqrt{2}\right] \end{array}\text{o}\right.</tex> <tex>\overline{\sigma}\left(t\right)=\left\{ \begin{array}{l} \left(\sqrt{2}\cos\left(t\right),\sqrt{2}\sen\left(t\right),2\right)\text{, con }t\in\left[0,2\pi\right]\\ \left(t,\sqrt{2-t^{2}},2\right)\text{, con }t\in\left[-\sqrt{2},\sqrt{2}\right] \end{array}\text{o}\right.</tex>](lib/plugins/latex/images/bbfe8954f94b37bb67580b252391f592d0de51bc_0.png)

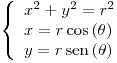
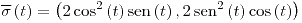

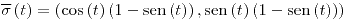
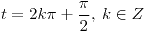
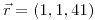
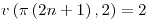 con
con 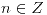
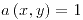
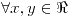

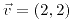
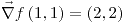
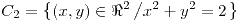
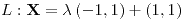

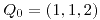
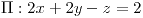
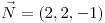


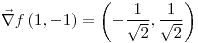
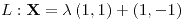

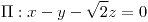
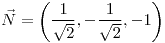


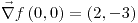
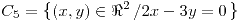
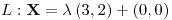

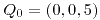
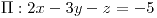
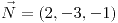

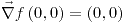



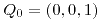
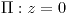

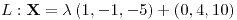
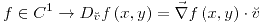
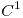
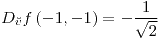
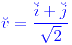
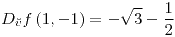
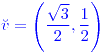
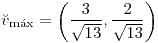 ;
; 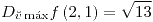
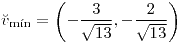 ;
; 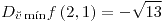
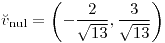 ;
; 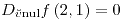
 ;
; 
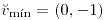 ;
; 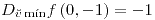
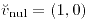 ;
; 
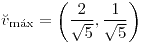 ;
; 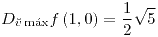
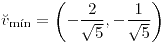 ;
; 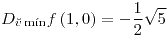
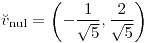 ;
; 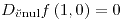
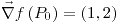

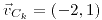
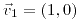 ;
; 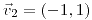 ;
; 
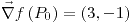
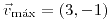
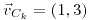
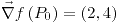
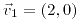 ;
; 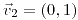 ;
; 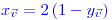
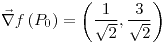

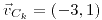
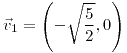 ;
; 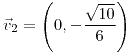
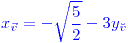
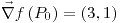

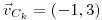
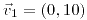 ;
; 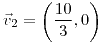 ;
; 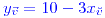
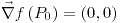
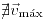 , la función no crece en
, la función no crece en 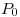
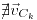 , es un punto
, es un punto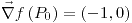
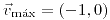
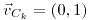
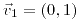 ; es la única dirección;
; es la única dirección; 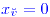
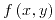 es diferenciable en todo punto ya que sus derivadas parciales son continuas:
es diferenciable en todo punto ya que sus derivadas parciales son continuas: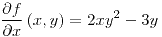 ,
, 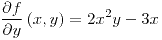
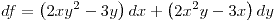
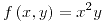 ,
, 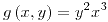 y
y  son funciones diferenciables por ser producto y suma de funciones diferenciables. Por lo tanto,
son funciones diferenciables por ser producto y suma de funciones diferenciables. Por lo tanto, 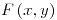 también lo es para todo punto (incluyendo
también lo es para todo punto (incluyendo 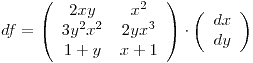
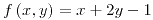
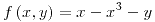
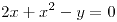 y el punto
y el punto 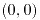 forma parte de esta ecuación, entonces
forma parte de esta ecuación, entonces 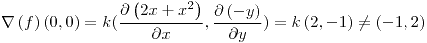 .
.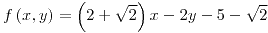

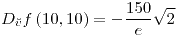 ;
; 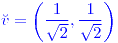

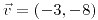 ;
; 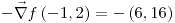
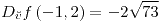 ;
; 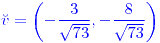
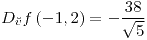 ;
; 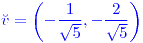
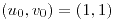
 ;
; 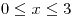 ;
; 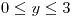

![<tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(1,1,1\right)+\lambda\left(1,0,-1\right)+\mu\left(0,1,-1\right)\\ x+y+z=3\text{ (cartesiana)} \end{array}</tex> <tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(1,1,1\right)+\lambda\left(1,0,-1\right)+\mu\left(0,1,-1\right)\\ x+y+z=3\text{ (cartesiana)} \end{array}</tex>](lib/plugins/latex/images/2597ecc5e98a9bc7d40a352be62f78de31e80289_0.png)
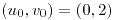
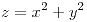 ;
; 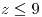

![<tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(0,2,4\right)+\lambda\left(1,0,0\right)+\mu\left(0,1,4\right)\\ 4y-z=4\text{ (cartesiana)} \end{array}</tex> <tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(0,2,4\right)+\lambda\left(1,0,0\right)+\mu\left(0,1,4\right)\\ 4y-z=4\text{ (cartesiana)} \end{array}</tex>](lib/plugins/latex/images/9911459ce4c6cc0b15356f29442879d675c0a1df_0.png)
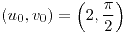

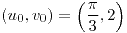
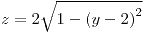 ;
; 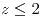 ;
; 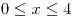
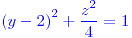

![<tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(2,\frac{3}{2},\sqrt{3}\right)+\lambda\left(1,0,0\right)+\mu\left(0,\frac{2}{\sqrt{3}},1\right)\\ \frac{2}{\sqrt{3}}y-z=0\text{ (cartesiana)} \end{array}</tex> <tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(2,\frac{3}{2},\sqrt{3}\right)+\lambda\left(1,0,0\right)+\mu\left(0,\frac{2}{\sqrt{3}},1\right)\\ \frac{2}{\sqrt{3}}y-z=0\text{ (cartesiana)} \end{array}</tex>](lib/plugins/latex/images/bc268b6720e01e1977b8a3edd57551189b4688d6_0.png)
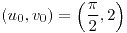
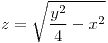 ;
; 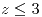
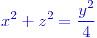

![<tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(0,4,2\right)+\lambda\left(1,0,0\right)+\mu\left(0,2,1\right)\\ y-2z=0\text{ (cartesiana)} \end{array}</tex> <tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(0,4,2\right)+\lambda\left(1,0,0\right)+\mu\left(0,2,1\right)\\ y-2z=0\text{ (cartesiana)} \end{array}</tex>](lib/plugins/latex/images/a3692e83c4431b2a98b3e487d187adfed580118c_0.png)
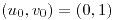
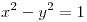 ;
; 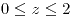

![<tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(1,0,1\right)+\lambda\left(1,0,1\right)+\mu\left(0,1,0\right)\\ x=1\text{ (cartesiana)} \end{array}</tex> <tex>\Pi:\begin{array}[t]{l} \mathbf{X}=\left(1,0,1\right)+\lambda\left(1,0,1\right)+\mu\left(0,1,0\right)\\ x=1\text{ (cartesiana)} \end{array}</tex>](lib/plugins/latex/images/8e36cb967a3f805bfca8c10e8ba7ae25ad23c9d5_0.png)
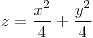
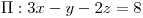
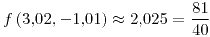
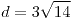





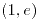 , por la tanto la composición
, por la tanto la composición 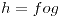 también es diferenciable en
también es diferenciable en 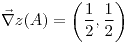

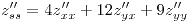
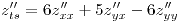








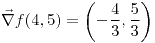
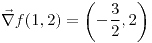

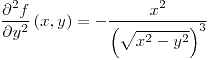
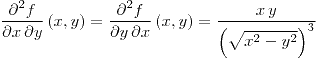
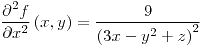
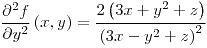
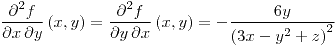
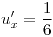 ,
,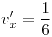 ,
, 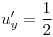 ,
,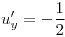
 ,
, 
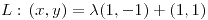
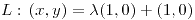
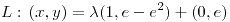

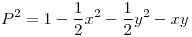
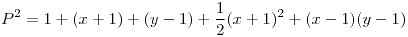
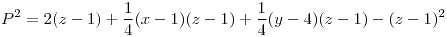
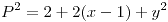
 .
.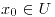 si
si  .
. .
.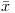 contiene puntos
contiene puntos  tales que
tales que 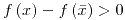 y puntos
y puntos  tales que
tales que 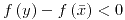 se dice que
se dice que 
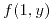 y
y 

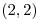 , puntos silla en
, puntos silla en 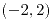 y
y  , máximo en
, máximo en 



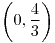 , puntos silla en
, puntos silla en  y
y 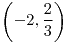 , máximo en
, máximo en 


![<tex>k \in [-2,2]</tex> <tex>k \in [-2,2]</tex>](lib/plugins/latex/images/1db457a047d73a6d7a4e8a1bd9d652de9ea4cbf1_0.png)
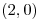 , puntos silla en
, puntos silla en  y
y 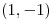 , máximo en
, máximo en 
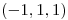 , máximo en
, máximo en 
 , punto silla en
, punto silla en 
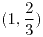
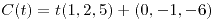 con
con 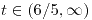 . Es simple.
. Es simple.
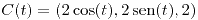 con
con  . Es simple.
. Es simple.
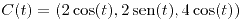 con
con ![<tex>t\in[0,\pi /2]</tex> <tex>t\in[0,\pi /2]</tex>](lib/plugins/latex/images/92580d77a6439bc45e47009e39265b9e4b75b20c_0.png) . Es simple.
. Es simple.
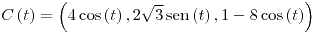 con
con 
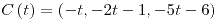 con
con 
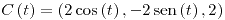 con
con 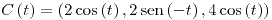 con
con ![<tex>t\in\left[-\frac{\pi}{2},0\right]</tex> <tex>t\in\left[-\frac{\pi}{2},0\right]</tex>](lib/plugins/latex/images/1258c1ca911b3200a7698d790fcfd4c772aee271_0.png)

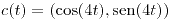 , con
, con 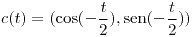 , con
, con ![<tex>t\in[0,4\pi]</tex> <tex>t\in[0,4\pi]</tex>](lib/plugins/latex/images/a6382e72a9ef9cddaa16b05c74622dd71725c9b5_0.png)
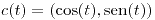 con
con 
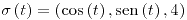 con
con 
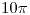
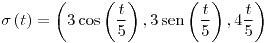 con
con ![<tex>t\in\left[0,10\pi\right]</tex> <tex>t\in\left[0,10\pi\right]</tex>](lib/plugins/latex/images/e56e637f506345c06c5baf8be9a7cdf554c27f33_0.png)
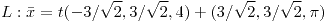







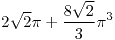


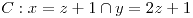






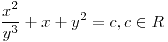





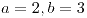 .
. 



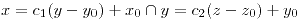
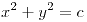






















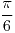





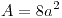
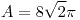
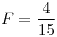 , con normal saliente
, con normal saliente

 , con normal saliente,
, con normal saliente, 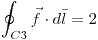
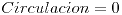
 ,
,