61.03 Análisis Matemático II - Recuperatorio - 14/11/2009
- Cátedra: Todas
- Fecha: 2° Oportunidad - (1° Cuatrimestre) 2009
- Día: 14/11/2009
- Tema: 1
Enunciado
1) Sea 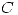 la curva plana descripta en coordenadas polares por
la curva plana descripta en coordenadas polares por 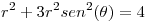 , graficar y encontrar, si es posible, un punto
, graficar y encontrar, si es posible, un punto 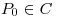 tal que la recta tangente a
tal que la recta tangente a  en
en 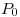 sea paralela al vector
sea paralela al vector 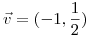
2) Sea 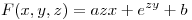 con
con  y
y 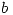
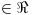 . Calcular
. Calcular  y
y  sabiendo que se cumplen simultáneamente:
-
sabiendo que se cumplen simultáneamente:
- 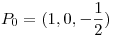 pertenece a la superficie de nivel 0 de
pertenece a la superficie de nivel 0 de  .
- El vector
.
- El vector 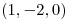 es tangente a la superficie de nivel 0 de
es tangente a la superficie de nivel 0 de  en
en 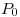 Además, justificar que
Además, justificar que 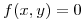 define implícitamente a
define implícitamente a  en un entorno de
en un entorno de 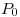 y calcular
y calcular 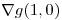
3) Sea  la superficie descripta en coordenadas cartesianas por
la superficie descripta en coordenadas cartesianas por 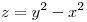 . Demostrar que la intersección de
. Demostrar que la intersección de  con su plano tangente en el punto
con su plano tangente en el punto 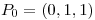 es un par de rectas.
es un par de rectas.
4) Sea 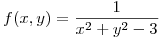 . Hallar el dominio y describir las curvas de nivel de
. Hallar el dominio y describir las curvas de nivel de  . Determinar extremos de
. Determinar extremos de  y clasificarlos justificando, además, si son relativos o absolutos.
y clasificarlos justificando, además, si son relativos o absolutos.
5) Sea 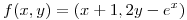 y
y 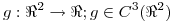 tal que el polinomio de Taylor de orden 2 de
tal que el polinomio de Taylor de orden 2 de 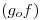 en el punto
en el punto  es
es 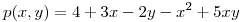 . Calcular la máxima derivada direccional de
. Calcular la máxima derivada direccional de  en el punto
en el punto 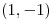 .
.
