Tabla de Contenidos
Examen Parcial - 61.03. Análisis Matemático II A
Cátedra: Acero
Fecha: Segunda Oportunidad - Primer Cuatrimestre 2005
Día: 28/05/2005
Esta página está incompleta; podés ayudar completando el material.
Enunciado
Punto I
Sea  la curva en
la curva en 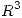 de ecuaciones
de ecuaciones 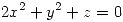 ,
,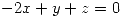 . Hallar una función
. Hallar una función 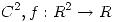 cuyo gráfico sea ortogonal a
cuyo gráfico sea ortogonal a  en el punto
en el punto 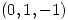 .
.
Punto II
Dadas en 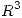 la curva
la curva  de ecuaciones
de ecuaciones 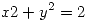 ,
, 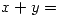 , y la curva
, y la curva  parametrizada por
parametrizada por 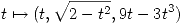 , hallar sus puntos de intersección en el primer octante, y mostrar que son perpendiculares en dichos puntos.
, hallar sus puntos de intersección en el primer octante, y mostrar que son perpendiculares en dichos puntos.
Punto III
Si el polinomio de Taylor de una función 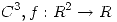 en
en  es:
es: 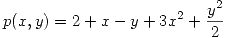 , hallar
, hallar  de manera que
de manera que 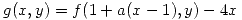 tenga un extremo local en
tenga un extremo local en  .
.
Punto IV
Resolver y fundamentar brevemente su respuesta:
- Sea
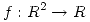 una función
una función  que es constante en la elipse de ecuación
que es constante en la elipse de ecuación 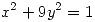 . Hallar
. Hallar 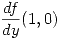
- Sea
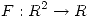 una función
una función 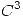 tal que
tal que 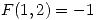 ,
, 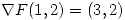 . Mostrar que si
. Mostrar que si 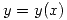 está definida por
está definida por 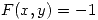 en un entorno de
en un entorno de 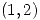 ,
,  es decreciente en
es decreciente en  .
.
Punto V
Hallar el área de la región plana descripta por: 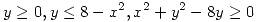 .
.
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
