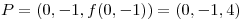61.03 Análisis Matemático II - Parcial - 02/05/2009
- Cátedra: Todas
- Fecha: 1° Oportunidad - (1° Cuatrimestre) 2009
- Día: 02/05/2009
Enunciado (abrir documento PDF)
Resolución
Punto 2
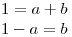
Sabemos que 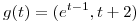 y que f es una función diferenciable tal que el plano tangente a su gráfica (1,3,4) es
y que f es una función diferenciable tal que el plano tangente a su gráfica (1,3,4) es . Además sabemos que
. Además sabemos que 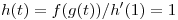 . Debemos averiguar los valores de a y b.
. Debemos averiguar los valores de a y b.
La primera coordenada de 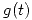 la llamamos 'x' y a la segunda 'y'.
la llamamos 'x' y a la segunda 'y'.
Con el dato 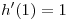 , podemos decir que
, podemos decir que  ; y si hacemos
; y si hacemos 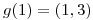 calculamos el punto en la función g.
calculamos el punto en la función g.
Ahora derivamos con la regla de la cadena:
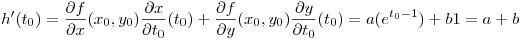
Entonces como 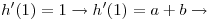
- Ecuación 1:
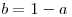
Luego sacamos la segunda condición de reemplazar el punto 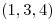 dado en la ecuación del plano dada:
dado en la ecuación del plano dada:
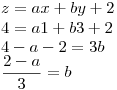
- Ecuación 2:
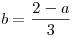
Igualando la ecuación 1 con la ecuación 2, obtenemos 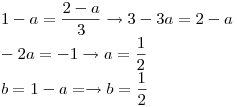
Entonces a=1/2 y b=1/2
Punto 5
Nos piden averiguar si ![<tex>g(x,y)=f(x,y)-sen[x(y+1)]</tex> <tex>g(x,y)=f(x,y)-sen[x(y+1)]</tex>](lib/plugins/latex/images/ad1b69ffe85b0b4edad9ee60ec3819936a299359_0.png) tiene un extremo en el punto
tiene un extremo en el punto 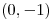 y analizarlo.
A simple vista vemos que la función
y analizarlo.
A simple vista vemos que la función 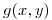 , depende de la función
, depende de la función 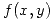 . Pero como nos dan el polinomio de Taylor de orden 2 de
. Pero como nos dan el polinomio de Taylor de orden 2 de 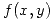 en el punto
en el punto 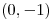 , podemos decir que en ese punto, la función y el polinimio de Taylor son iguales.
, podemos decir que en ese punto, la función y el polinimio de Taylor son iguales.
Polinomio (dato): 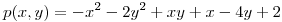
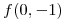 ≅
≅
Ahora calculamos las derivadas parciales de primer orden para el polinomio de Taylor (para que existan extremos deben ser igual a cero en el punto a evaluar):
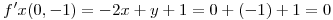
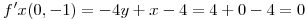
Ahora calculamos las derivadas parciales de segundo orden para el polinomio de Taylor:

 | Por el Teorema de Schwarz (la función debe ser diferenciable, es decir admitir derivadas parciales continuas)
| Por el Teorema de Schwarz (la función debe ser diferenciable, es decir admitir derivadas parciales continuas)
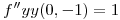
Con estos datos calculamos la matriz Hessiana (para evaluar los extremos de la función) en el punto pedido.
![<tex>g(0,-1)=f(0,-1)-sen[0(-1+1)]=4-sen(0)=4</tex> <tex>g(0,-1)=f(0,-1)-sen[0(-1+1)]=4-sen(0)=4</tex>](lib/plugins/latex/images/a0c2fc8352aab2a2921db2db2b2c8c5fd23e77a9_0.png)
=0-cos[0(-1+1)](-1+1)=0</tex> <tex>g'x(0,-1)=f'x(0,-1)-cos[x(y+1)](y+1)=0-cos[0(-1+1)](-1+1)=0</tex>](lib/plugins/latex/images/3c5e7a1f877d83848bfec65629c525c31ffe364a_0.png)
![<tex>g'y(0,-1)=f'y(0,-1)-cos[x(y+1)]x=0-cos[0(-1+1)]x=0</tex> <tex>g'y(0,-1)=f'y(0,-1)-cos[x(y+1)]x=0-cos[0(-1+1)]x=0</tex>](lib/plugins/latex/images/6293ec1bcd7094e2ca1e21fca007bc38b7a8b638_0.png)
](y+1)](y+1)=</tex> <tex>g''xx(0,-1)=f''xx(0,-1)-[-sen[x(y+1)](y+1)](y+1)](y+1)=</tex>](lib/plugins/latex/images/f9f587adb1d3cd94153dce674a3d6476fd40735b_0.png)
=-2+0=-2</tex> <tex>-2+sen[0(-1+1)](-1+1)=-2+0=-2</tex>](lib/plugins/latex/images/30fb12a89c6a2917c58cdcbb3530e597c384e35b_0.png)
![<tex>g''xy(0,-1)=f''xy(0,-1)-[-sen[x(y+1)]x(y+1)]+cos[x(y+1)]=</tex> <tex>g''xy(0,-1)=f''xy(0,-1)-[-sen[x(y+1)]x(y+1)]+cos[x(y+1)]=</tex>](lib/plugins/latex/images/7557db51a0f7ea30961a62098b6c5ebb9d11cd37_0.png)
![<tex> = 1-[-sen[0(-1+1)0(-1+1)+cos[0(-1+1)]=1+sen(0)+cos(0)=2</tex> <tex> = 1-[-sen[0(-1+1)0(-1+1)+cos[0(-1+1)]=1+sen(0)+cos(0)=2</tex>](lib/plugins/latex/images/c04d1c31ca3bc9efa6fb47550c7cca9dda4abe99_0.png)
![<tex>g''yy(0,-1)=f''yy(0,-1)-[-sen[x(y+1)]x(y+1)]+cos[x(y+1)]1=</tex> <tex>g''yy(0,-1)=f''yy(0,-1)-[-sen[x(y+1)]x(y+1)]+cos[x(y+1)]1=</tex>](lib/plugins/latex/images/c9f5f6d4bb6e6c1a6355c940b0133a2a34616c70_0.png)
![<tex> =-4-[-sen[0(-1+1)0(-1+1)+cos[0(-1+1)]=-4+sen(0)+cos(0)=-4</tex> <tex> =-4-[-sen[0(-1+1)0(-1+1)+cos[0(-1+1)]=-4+sen(0)+cos(0)=-4</tex>](lib/plugins/latex/images/0dd1ac16744c268876325d23af52520a17593ab5_0.png)
Utilizo estos datos para determinar el extremo mediante la matriz Hessiana:
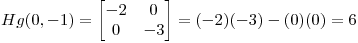
Como 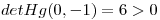 y
y 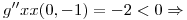 Máximo local
Máximo local