Parcial - 61.03 Análisis Matemático II - 11/10/2008
Cátedra: Todas
Fecha: 1° Oportunidad - (2° Cuatrimestre) 2008
Día: 11/10/2008
Enunciado
1) Sea 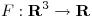 una función
una función 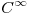 tal que
tal que 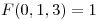 y
y 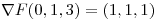 .
.
Hallar la ecuación de la recta perpendicular a la superficie 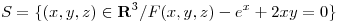 en el punto
en el punto 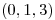
2) Mostrar que el sistema 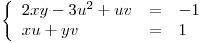 define
define 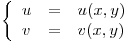 en el entorno del punto
en el entorno del punto 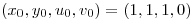 y hallar el plano tangente a la gráfica de la función
y hallar el plano tangente a la gráfica de la función 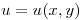 en el punto
en el punto 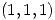
3) Sea 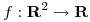 una función
una función 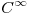 cuyo polinomio de Taylor de orden 2 en el punto
cuyo polinomio de Taylor de orden 2 en el punto  es
es 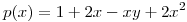 .
Sea
.
Sea 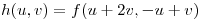 . Hallar el valor de la derivada direccional máxima de
. Hallar el valor de la derivada direccional máxima de 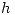 en
en 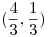 .
.
4) Hallar  de modo que la recta
de modo que la recta 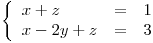 sea tangente en
sea tangente en 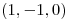 a la superficie parametrizada por
a la superficie parametrizada por 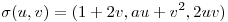 con
con 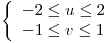 .
.
5) Sea la superficie  definida por
definida por 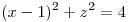 hallar y parametrizar una curva
hallar y parametrizar una curva 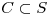 de manera que
de manera que  resulte perpendicular al vector
resulte perpendicular al vector 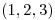 en todo punto.
en todo punto.
Resolución
Punto I
1) Defino 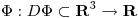 tal que
tal que 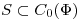
El 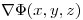 será normal a
será normal a 
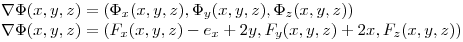
Es dato: 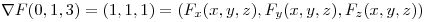
Reemplazo para el punto (0,1,3), que es donde quiero la normal a la superficie:
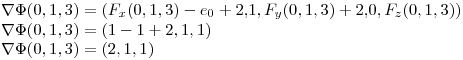
La recta será entonces: 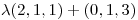
Punto 2
La ecuación del plano tangente será: 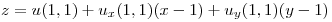
Quiero usar el teorema de Cauchi-Dinni (hay que verificar las condiciones)
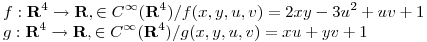
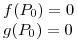
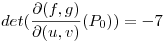
Verificadas las hipótesis puedo operar: