Parcial - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: 1er Recuperatorio - 1er Cuatrimestre 2008
Día: 24/05/2008
Enunciado
1) Sea 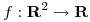 y su polinomio de Taylor de orden 2 en
y su polinomio de Taylor de orden 2 en 
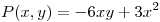 Y sea
Y sea 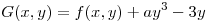
Hallar a para que  tenga un minimo en
tenga un minimo en 
2) Sea una superficie 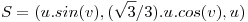 y PI un plano de ecuacion
y PI un plano de ecuacion 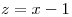 . Hallar todos los puntos de S en los que su recta normal es paralela al plano PI.
. Hallar todos los puntos de S en los que su recta normal es paralela al plano PI.
3) Sea 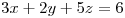 el plano tangente a la grafica
el plano tangente a la grafica 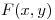 en
en 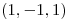 ,
,
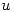 el versor tangente a la curva de nivel 9 de
el versor tangente a la curva de nivel 9 de 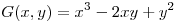 en
en 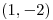 .
Hallar la derivada direccional de
.
Hallar la derivada direccional de  en la direccion de
en la direccion de 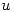 .
.
4) 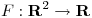 es
es  Demostrar que se cumple
Demostrar que se cumple 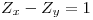 en un entorno de
en un entorno de 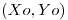 .
.
5) La curva  esta deterimnada por la interseccion del cilindro
esta deterimnada por la interseccion del cilindro 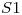 , cuya proyeccion en el plano
, cuya proyeccion en el plano  es la curva parametrizada en coordenadas polares por
es la curva parametrizada en coordenadas polares por 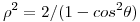 , y el cilindro
, y el cilindro 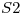 , definido en coordenadas cartesianas por
, definido en coordenadas cartesianas por 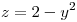 .
.
a) Describir la curva, intersección 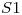 y
y 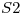 . Dar una parametrizacion para
. Dar una parametrizacion para  y graficarla aproximadamente.
y graficarla aproximadamente.
b) Obtener el vector tangente a  en el punto
en el punto 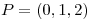 .
.
