Examen Parcial - 61.03. Análisis Matemático II A - 08/05/2008
Cátedra: Indistinta
Fecha: 1° Oportunidad - 1° Cuatrimestre 2008
Día: 08/05/2008
Tema: 2
Enunciado
Punto I
Sea 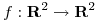 una función diferenciable,
una función diferenciable, 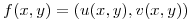 tal que
tal que 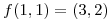 , con matriz jacobiana de
, con matriz jacobiana de 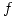 en
en 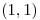 :
:
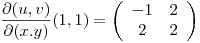
Sea 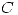 la Curva imagen por
la Curva imagen por 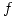 de
de 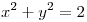 . Hallar la ecuación de la recta tangente a
. Hallar la ecuación de la recta tangente a 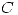 en
en 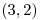 .
.
Punto II
Una función 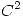
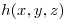 tiene un máximo relativo de valor 0 en
tiene un máximo relativo de valor 0 en 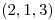 . Hallar una ecuación del plano tangente en
. Hallar una ecuación del plano tangente en 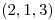 a la superficie de ecuación
a la superficie de ecuación  .
.
Punto III
Parametrizar la curva
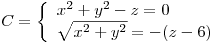
Graficar 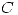 y hallar la ecuación de la recta tangente a la curva de nivel en el punto
y hallar la ecuación de la recta tangente a la curva de nivel en el punto 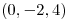
Punto IV
Sabiendo que:

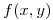 es una función diferenciable en
es una función diferenciable en 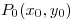
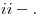 La recta de ecuación
La recta de ecuación 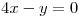 es perpendicular a la curva de nivel de
es perpendicular a la curva de nivel de 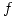 que pasa por
que pasa por 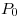
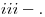 La máxima pendiente de la superficie
La máxima pendiente de la superficie 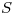 de ecuación
de ecuación 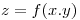 en
en 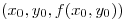 es
es 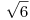 .
.
Hallar el gradiente de 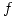 en
en 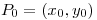 sabiendo que su primer componente es positiva.
sabiendo que su primer componente es positiva.
Punto V
Hallar 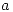 para que las superficies:
para que las superficies:
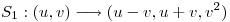 con
con 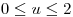 y
y 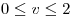
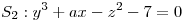 sean ortogonales en el punto
sean ortogonales en el punto